
题目列表(包括答案和解析)
20.(本小题共13分)
对于每项均是正整数的数列![]() ,定义变换
,定义变换![]() ,
,![]() 将数列
将数列![]() 变换成数列
变换成数列
![]()
![]() .
.
对于每项均是非负整数的数列![]() ,定义变换
,定义变换![]() ,
,![]() 将数列
将数列![]() 各项从大到小排列,然后去掉所有为零的项,得到数列
各项从大到小排列,然后去掉所有为零的项,得到数列![]() ;
;
又定义![]() .
.
设![]() 是每项均为正整数的有穷数列,令
是每项均为正整数的有穷数列,令![]() .
.
(Ⅰ)如果数列![]() 为5,3,2,写出数列
为5,3,2,写出数列![]() ;
;
(Ⅱ)对于每项均是正整数的有穷数列![]() ,证明
,证明![]() ;
;
(Ⅲ)证明对于任意给定的每项均为正整数的有穷数列![]() ,存在正整数
,存在正整数![]() ,当
,当![]() 时,
时,![]() .
.
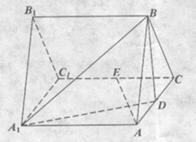
(本小题满分13分)如图,三棱柱ABC—A1B1C1的所有棱长都是2,又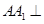 平面
平面
ABC,D、E分别是AC、CC1的中点。
(1)求证: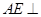 平面A1BD;
平面A1BD;
(2)求二面角D—BA1—A的余弦值;
(3)求点B1到平面A1BD的距离。
设 是两个不共线的非零向量.
是两个不共线的非零向量.
(1)若 =
= ,
, =
= ,
, =
= ,求证:A,B,D三点共线;
,求证:A,B,D三点共线;
(2)试求实数k的值,使向量 和
和 共线. (本小题满分13分)
共线. (本小题满分13分)
【解析】第一问利用 =(
=( )+(
)+( )+
)+ =
= =
= 得到共线问题。
得到共线问题。
第二问,由向量 和
和 共线可知
共线可知
存在实数 ,使得
,使得 =
= (
( )
)
 =
= ,结合平面向量基本定理得到参数的值。
,结合平面向量基本定理得到参数的值。
解:(1)∵ =(
=( )+(
)+( )+
)+
= =
= ……………3分
……………3分
∴  ……………5分
……………5分
又∵ ∴A,B,D三点共线 ……………7分
∴A,B,D三点共线 ……………7分
(2)由向量 和
和 共线可知
共线可知
存在实数 ,使得
,使得 =
= (
( )
……………9分
)
……………9分
∴ =
= ……………10分
……………10分
又∵ 不共线
不共线
∴ ……………12分
……………12分
解得
((本小题满分13分)设O为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P、Q关于直线x+my+4=0对称,又满足OP⊥OQ.
(1)求m的值;
(2)求直线PQ的方程.
(本大题13分)设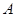 、
、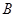 为函数
为函数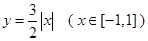 图象上不同的两个点,
图象上不同的两个点,
且 AB∥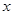 轴,又有定点
轴,又有定点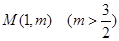 ,已知
,已知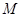 是线段
是线段 的中点.
的中点.
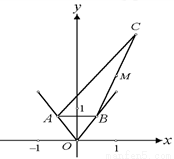
⑴ 设点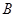 的横坐标为
的横坐标为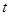 ,写出
,写出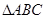 的面积
的面积 关于
关于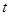 的函数
的函数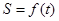 的表达式;
的表达式;
⑵ 求函数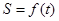 的最大值,并求此时点
的最大值,并求此时点 的坐标。
的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com