已知函数.

(Ⅰ)若值点，求a的值；

(Ⅱ）求证：当0<a≤2时，f(x)在上是增函数；

（Ⅲ）若对任意的,总存在,使不等式成立，求实数m的取值范围.

已知函数f(x)=mx³+nx²(m、n∈R ,m≠0)的图像在（2，f(2)）处的切线与x轴平行.

（1）求n,m的关系式并求f(x)的单调减区间；

（2）证明：对任意实数0<x₁<x₂<1, 关于x的方程：

在（x₁,x₂）恒有实数解

（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f(x)是在闭区间[a,b]上连续不断的函数，且在区间(a,b)内导数都存在，则在(a,b)内至少存在一点x₀，使得.如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明：

当0<a<b时，（可不用证明函数的连续性和可导性）

已知函数f(x)在(－1，1)上有定义，f()=－1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(－1,1)都有f(x)+f(y)=f(),试证明：w.w.w.k.s.5.u.c.o.m       

(1)f(x)为奇函数；(2)f(x)在(－1，1)上单调递减.

已知函数，．

（Ⅰ）若函数和函数在区间上均为增函数，求实数的取值范围；

（Ⅱ）若方程有唯一解，求实数的值．

【解析】第一问，   

当0<x<2时，，当x>2时，，

要使在(a,a+1)上递增，必须

如使在(a,a+1)上递增，必须，即

由上得出，当时，在上均为增函数

（Ⅱ）中方程有唯一解有唯一解

设  （x>0）

随x变化如下表

x
	-		+
		极小值

由于在上，只有一个极小值，的最小值为-24-16ln2，

当m=-24-16ln2时，方程有唯一解得到结论。

（Ⅰ）解： 

当0<x<2时，，当x>2时，，

要使在(a,a+1)上递增，必须

如使在(a,a+1)上递增，必须，即

由上得出，当时，在上均为增函数  ……………6分

（Ⅱ）方程有唯一解有唯一解

设  （x>0）

随x变化如下表

x
	-		+
		极小值

由于在上，只有一个极小值，的最小值为-24-16ln2，

当m=-24-16ln2时，方程有唯一解

 

已知y＝x(x－1)(x＋1)的图像如图所示，今考虑f(x)＝x(x－1)(x＋1)＋0.01，对于方程式f(x)＝0根的情况，以下说法正确的是________．(填上正确的序号)

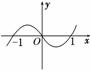①有三个实根；

②当x<－1时，恰有一实根；

③当－1<x<0时，恰有一实根；

④当0<x<1时，恰有一实根；

⑤当x>1时，恰有一实根．