
题目列表(包括答案和解析)
.(本小题满分13分)
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数f(x)模型制定奖励方案,试用数学语言表述公司对奖励函数f(x)模型
的基本要求;
(2)现有两个奖励函数模型:(1)y= ;(2)y=4lgx-3.试分析这两个函数模型
;(2)y=4lgx-3.试分析这两个函数模型
是否符合公司要求?
(本小题满分13分) 记函数 的定义域为集合M,函数
的定义域为集合M,函数 的定义域为集合N,集合C={x|m-1<x<m+1,m∈R}求:
的定义域为集合N,集合C={x|m-1<x<m+1,m∈R}求:
(1)集合 ,
, (2)若
(2)若 ,求实数m的取值范围
,求实数m的取值范围
(本小题满分13分)
已知正项数列{an}的首项a1=,函数f(x)=,g(x)=.
(1)若正项数列{an}满足an+1=f(an)(n∈N*),证明:{}是等差数列,并求数列{an}的通项公式;
(2)若正项数列{an}满足an+1≤f(an)(n∈N*),数列{bn}满足bn=,证明:b1+b2+…+bn<1;
(3)若正项数列{an}满足an+1=g(an),求证:|an+1-an|≤·()n-1
(本小题满分13分)
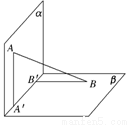
如图,平面α⊥平面β,A∈α,B∈β,AB与平面α、β所成的角分别为和,过A、B分别作两平面交线的垂线,垂足为A′、B′,若AB=12,求A′B′的长度.
(本小题满分13分)
已知f(x)=mx(m为常数,m>0且m≠1).
设f(a1),f(a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列.
(1)求证:数列{an}是等差数列;
(2)若bn=an·f(an),且数列{bn}的前n项和为Sn,当m=2时,求Sn;
(3)若cn=f(an)lgf(an),问是否存在m,使得数列{cn}中每一项恒小于它后面的项?若存在,
求出m的范围;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com