（本小题共12分）已知抛物线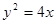的焦点是F，点P是抛物线上的动点，又有点A（3,2），求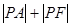最小值，并求此时P点的坐标.

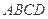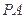（本小题满分12分）如图，在矩形中，，又⊥平面，．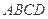
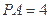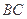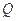（Ⅰ）若在边上存在一点，使，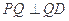
求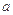的取值范围；
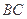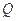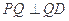（Ⅱ）当边上存在唯一点，使时，
求二面角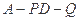的余弦值．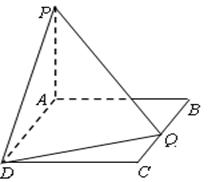

（本小题满分12分）

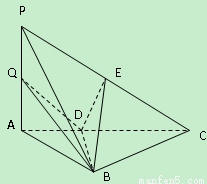
如图，三棱锥P-ABC中，PA⊥底面ABC，AB⊥BC，DE垂直平分PC，且分别交AC、PC于D、E两点，又PB=BC，PA=A B．

（Ⅰ）求证：PC⊥平面BDE；

（Ⅱ）若点Q是线段PA上任一点，求证：BD⊥DQ；

（Ⅲ）求线段PA上点Q的位置，使得PC//平面BDQ．

（本题满分12分）

如图，四边形是直角梯形，∠＝90°，∥，＝1，＝2，又＝1，

∠＝120°，⊥，直线与直线所成的角为60°.

（Ⅰ）求证：平面⊥平面；

（Ⅱ）求三棱锥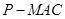的体积；

(12分)某银行准备新设一种定期存款业务，经预测，存款量与存款利率的平方成正比，比例系数为，且知当利率为0.012时，存款量为1.44亿；又贷款的利率为时，银行吸收的存款能全部放贷出去；若设存款的利率为，，试写出存款量f(x)与存款利率的关系式，且当为多少时，银行可获得最大收益？（收益指银行放贷所得利息与付给储户存款利息之差）