练习册

  • 练习册
  • 试题
    如图11 所示.以RtΔABC的直角边AB为直径作圆O.与斜边交于点D,E为BC边上的中点.连接DE.(1)求证:DE是⊙O的切线, 【查看更多】

     

    题目列表(包括答案和解析)

    ．（本题满分10分）

    如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．

    1.（1）求证：△ADF∽△DEC：

    2.（2）若AB=4，AD=3，AE=3，求AF的长．

     

    查看答案和解析>>

    （本题满分10分）如图，在平面直角坐标系中，O为坐标原点，P是反比例函数

    y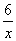＝（x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、

    B．

    （1）判断P是否在线段AB上，并说明理由；

    （2）求△AOB的面积；

    （3）Q是反比例函数y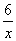＝（x＞0）图象上异于点P的另一点，请以Q为圆心，QO

     半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．

     

     

     

     

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    （本题满分10分）

    如图，已知一次函数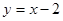与反比例函数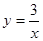的图象交于A、B两点．

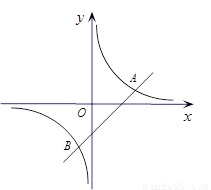
    （1）求A、B两点的坐标；

    （2）观察图象，可知一次函数值小于反比例函数值的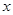的取值范围是  ▲  ．（把答案直接写在答题卡相应位置上）

     

    查看答案和解析>>

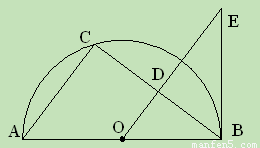
    （11·永州）（本题满分10分）如图，AB是半圆O的直径，点C是⊙O上一点

    （不与A，B重合），连接AC，BC，过点O作OD∥AC交BC于点D，在OD的延长线上

    取一点E，连接EB，使∠OEB=∠ABC．

    ⑴ 求证：BE是⊙O的切线；

    ⑵ 若OA=10，BC=16，求BE的长．

     

    查看答案和解析>>

    （本题满分10分）

    如图，AB是⊙O的直径，点C是BA延长线上一点，CA=1，CD切⊙O于D点，弦DE∥CB，Q是AB上一动点，当DQ⊥AB时Q恰好为OA中点.

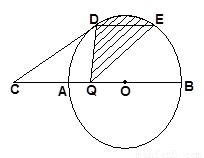
    1. (1)求⊙O的半径R．

    2.(2) 当点 Q从点A向点B运动的过程中，图中阴影部分的面积是否发生变化，若发生变化，请你说明理由；若不发生变化，请你求出阴影部分的面积．

     

    查看答案和解析>>

    一

    1. C   2. B   3.D   4.B  5.D   6.C  7. C   8. C   9.D   10.A 

    二

    11.4

    12.y=2（x+3）2-7

    13.

    14.3

    15.153

    16.9800

    三

    17.解:原式=                     ………    2分

    ∵x≠0且x≠且x≠2                                      ………  3分

    ∴x=-1                                                 …………… 4分

    ∴原式==-                                  ………… 5分

    18.（1）答案不惟一，例如四个图案具有的共同特征可以是：①都是轴对称图形；②面积都等于四个小正方形的面积之和；③都是直线形图案。。。。。只要写出两个即可。…… 3分

    （2）答案示例：


    ……  6分

    19.已知：如图所示，AD为ΔABC的中线，且CF⊥AD于F,BE⊥AD的延长线于E.

    求证;BE=CF.

    证明：∵AD为ΔABC的中线。                                

    ∴BD=CD.              ………  1分

    ∵BE⊥AD,CF⊥AD.

    ∴∠BED=∠CFD=90º .  ………  3分

    又∠1=∠2.

    ∴ΔBED≌ΔCFD(AAS).     ……… 5分

    BE=CF                  ……… 7分

    (本题还可以作AN⊥BC于N，利用等底等高的两个三角形的面积相等的性质证明)

    20.（1）A品牌牙膏主要竞争优势是质量，①对A品牌牙膏的质量满意的最多；②对A品牌牙膏的广告，价格满意的不是最多；③对A品牌牙膏购买的人最多 

    ∴ A品牌牙膏靠的是质量优势     ……………2分

    （2）广告对用户选择品牌有影响，原因是：①对B,C牙膏的质量，价格满意的用户，相差不大；②对B品牌的广告，满意的用户比C多，相差较大;③购买B品牌的用户高于C.

       ∴广告影响用户选择品牌 。    ………………………………….      5分

    （3）首先要提高质量，其次加大广告力度，最后注意合理的价格。……………      8分

    21.（1）34.5元                    ………………………      2分

    （2）35.5元，28.5元             ………………………     4分

    （3）1331.25元                   ………………………     8分

    22．羊可以吃到的草的最大面积由三部分组成：第一部分：以点A为圆心，12米为半径。圆心角为60°的扇形的面积减去三角形ABC的面积；第二部分：以点B为圆心，6米为半径，圆心角为60°的扇形面积；第三部分与第二部分相等。  ………………    3分

    因此，羊可以吃到的草的面积是：

    （平方米）    ……………  8分

    23.解;根据题意易知，水柱上任意一个点距中心的水平距离为x，与此点的

    高度y之间的函数关系式是：      ...............          1分

    Y=a1(x+4)2+6 (-10≤x＜0 ）或 y=a2(x+4)2+6 （0≤x≤10）.....   3分

    由x=-10，y=0, 可得a1=-; 由x=10, y=0, 可得a2=-  .....   5分 

    于是，所求函数解析式是 Y=-(x+4)2+6 (-10≤x＜0 ）

    y=-(x+4)2+6（0≤x≤10）     ………  6分

        当x=0时，y=             

        所以装饰物的高度为m   ………  8分

    24.（1）连接O,D与B,D两点。

    ∵ΔBDC是RtΔ, 且E为BC中点。

    ∴∠EDB=∠EBD.         ………    2分

    又∵OD=OB  且∠EBD+∠DBO=90°       

    ∴∠EDB+∠ODB=90°

    ∴DE是⊙O的切线；       ……    4分

    （2）∵∠EDO=∠B=90°,

    若要AOED是平行四边形，则DE∥AB,D为AC中点。

    又∵BD⊥AC,

    ∴ΔABC为等腰直角三角形。

    ∴∠CAB=45°.         ……     6分    

    过E作EH⊥AC于H.

    设BC=2k，

    则EH=  ………  8分

    ∴sin∠CAE=    ……  10分

    25.(1) ?i    1                       …2分.

    (2)①5   ②3+4i                    …4分

    (3)已知（x+y）+3i=1-(x+y)i

    可得（x+y）+3i=(1-x)-yi         …5分

    ∴x+y=1-x, 3=-y                  …6分

    ∴x=2   y=-3                     …   8分

    (4)解原式：=    …   12分

     


    同步练习册答案