
题目列表(包括答案和解析)

 ≈1.8,
≈1.8,  ≈1.9,
≈1.9,  ≈2.1).
≈2.1).[应用题]如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一绳子的两端拴于立柱与铁杠结合处,绳子自然下垂呈抛物线状.
(1)如图(1)一身高为0.7米的小孩站在离立柱0.4米处,其头部刚好触到绳子,求绳子最低点到地面的距离;
(2)如图(2),为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板.除掉系木板用去的绳子后,两边的绳子长正好各为2米,木板与地面平行.求这时木板离地面的距离(参考数据:≈1.8,
≈1.9,
≈2.1).
[应用题]如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一绳子的两端拴于立柱与铁杠结合处,绳子自然下垂呈抛物线状.
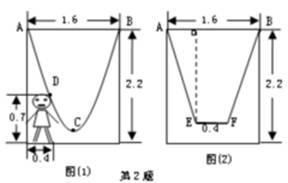
(1)如图(1)一身高为0.7米的小孩站在离立柱0.4米处,其头部刚好触到绳子,求绳子最低点到地面的距离;
(2)如图(2),为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板.除掉系木板用去的绳子后,两边的绳子长正好各为2米,木板与地面平行.求这时木板离地面的距离(参考数据: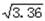 ≈1.8,
≈1.8,  ≈1.9,
≈1.9, 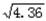 ≈2.1).
≈2.1).
[应用题]如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一绳子的两端拴于立柱与铁杠结合处,绳子自然下垂呈抛物线状.
(1)如图(1)一身高为0.7米的小孩站在离立柱0.4米处,其头部刚好触到绳子,求绳子最低点到地面的距离;
(2)如图(2),为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板.除掉系木板用去的绳子后,两边的绳子长正好各为2米,木板与地面平行.求这时木板离地面的距离(参考数据: ≈1.8,
≈1.8, 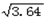 ≈1.9,
≈1.9,  ≈2.1).
≈2.1).
 ≈1.8,
≈1.8, ≈1.9,
≈1.9, ≈2.1)。
≈2.1)。
一.选择题
1. B 2.D 3.C 4.A 5.D 6.D 7.C 8.C 9.C 10.C
二.填空题
11.%20.files/image158.gif) 12. 3858 13.
12. 3858 13.%20.files/image160.gif) ; 14.
; 14.%20.files/image162.gif) 15. 5n+3或3(2n+1)-n
15. 5n+3或3(2n+1)-n
16. 1;提示:(-1)×(-3)-2=3-2=1
三.解答题
17.解:原式=(%20.files/image164.gif) )?
)?%20.files/image166.gif) =
=%20.files/image168.gif)
%20.files/image166.gif) =x+2
=x+2
把x=%20.files/image111.gif) +1代入上式得:原式=
+1代入上式得:原式=%20.files/image111.gif) +3
+3
18.(1)43 (2)略 (3) -4 , 1
19.证CD=DE=CB=BE
%20.files/image175.gif) 这次考察中一共调查了60名学生.
这次考察中一共调查了60名学生.
(2)%20.files/image177.gif) ,
,
%20.files/image179.gif) ,
,
%20.files/image181.gif) 在扇形统计图中,“乒乓球”
在扇形统计图中,“乒乓球”
部分所对应的圆心角为%20.files/image183.gif) .
.
(3)%20.files/image185.gif) 补全统计图如图:
补全统计图如图:
(4)%20.files/image187.gif) ,
,
%20.files/image181.gif) 可以估计该校学生喜欢篮球活动的约有450人.
可以估计该校学生喜欢篮球活动的约有450人.
21.解:(1)设2006年平均每天的污水排放量为%20.files/image021.gif) 万吨,则2007年平均每天的污水排放量为1.05x万吨,依题意得:
万吨,则2007年平均每天的污水排放量为1.05x万吨,依题意得:
解得%20.files/image193.gif)
经检验,%20.files/image193.gif) 是原方程的解.
是原方程的解.
%20.files/image196.gif)
答:2006年平均每天的污水排放量约为56万吨,2007年平均每天的污水排放量约为59万吨.
(2)解:设2010年平均每天的污水处理量还需要在2007年的基础上至少增加%20.files/image023.gif) 万吨,依题意得:
万吨,依题意得:
%20.files/image199.gif)
解得%20.files/image201.gif)
答:2010年平均每天的污水处理量还需要在2007年的基础上至少增加%20.files/image203.gif) 万吨.
万吨.
22.(1)P(一等奖)=%20.files/image204.gif) ;P(二等奖)=
;P(二等奖)=%20.files/image205.gif) ,P(三等奖)=
,P(三等奖)=%20.files/image206.gif) ;
;
(2)%20.files/image207.gif)
%20.files/image208.gif)
∴活动结束后至少有5000元赞助费用于资助贫困生。
23.解:(1)在%20.files/image210.gif) 和
和%20.files/image212.gif) 中,
中,
%20.files/image214.gif) ,
,%20.files/image139.gif) ,
,%20.files/image217.gif) .??????????????????????????????????????????????? 2分
.??????????????????????????????????????????????? 2分
%20.files/image225.gif) 又
又%20.files/image227.gif) ,
,
%20.files/image229.gif) .????????????????? 4分
.????????????????? 4分
(2)直线%20.files/image147.gif) 与
与%20.files/image129.gif) 相切.
相切.
证明:连结%20.files/image233.gif) .
.
%20.files/image235.gif) ,
,
%20.files/image237.gif) .??????????????????? 5分
.??????????????????? 5分
%20.files/image239.gif) .
.
所以%20.files/image241.gif) 是等腰三角形
是等腰三角形%20.files/image243.gif) 顶角
顶角%20.files/image245.gif) 的平分线.
的平分线.
%20.files/image247.gif) .??????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
.??????????????????????????????????????????????????????????????????????????????????????????????????????? 6分
由%20.files/image149.gif) ,得
,得%20.files/image250.gif) .
.%20.files/image252.gif) .?????????????????????????????????? 7分
.?????????????????????????????????? 7分
由%20.files/image254.gif) 知,
知,%20.files/image256.gif) .
.%20.files/image258.gif) 直线
直线%20.files/image260.gif) 与
与%20.files/image129.gif) 相切.?????????????????????????????????????????? 8分
相切.?????????????????????????????????????????? 8分
24.解:(1)如图,建立直角坐标系,设二次函数解析式为y=ax2+c
∵ D(-0.4,0.7),B(0.8,2.2),
%20.files/image261.gif) ∴
∴ %20.files/image263.gif) 解得:
解得:%20.files/image265.gif)
∴绳子最低点到地面的距离为
(2)分别作EG⊥AB于G,FH⊥AB于H,
AG=%20.files/image158.gif) (AB-EF)=
(AB-EF)=%20.files/image158.gif) (1.6-0.4)=0.6.
(1.6-0.4)=0.6.
在Rt△AGE中,AE=2,
EG=%20.files/image268.gif) =
=%20.files/image270.gif) =
=%20.files/image272.gif) ≈1.9.
≈1.9.
∴ 2.2-1.9=0.3(米). ∴ 木板到地面的距离约为
25.解:⑴ 解法一:设%20.files/image274.gif) ,
,
任取x,y的三组值代入,求出解析式%20.files/image276.gif) ,
,
令y=0,求出%20.files/image278.gif) ;令x=0,得y=-4,
;令x=0,得y=-4,
∴ A、B、C三点的坐标分别是A(2,0),B(-4,0),C(0,-4) .
解法二:由抛物线P过点(1,-%20.files/image154.gif) ),(-3,
),(-3,%20.files/image281.gif) )可知,
)可知,
抛物线P的对称轴方程为x=-1,
又∵ 抛物线P过(2,0)、(-2,-4),则由抛物线的对称性可知,
点A、B、C的坐标分别为 A(2,0),B(-4,0),C(0,-4) .
⑵ 由题意,%20.files/image283.gif) ,而AO=2,OC=4,AD=2-m,故DG=4-
,而AO=2,OC=4,AD=2-m,故DG=4-
又 %20.files/image285.gif) ,EF=DG,得BE=4-
,EF=DG,得BE=4-
∴SDEFG=DG?DE=(4-
⑶ ∵SDEFG=
当矩形面积最大时,其顶点为D(1,0),G(1,-2),F(-2,-2),E(-2,0),
设直线DF的解析式为y=kx+b,易知,k=%20.files/image287.gif) ,b=-
,b=-%20.files/image287.gif) ,∴
,∴%20.files/image289.gif) ,
,
又可求得抛物线P的解析式为:%20.files/image276.gif) ,
,
令%20.files/image292.gif) =
=%20.files/image294.gif) ,可求出x=
,可求出x=%20.files/image296.gif) . 设射线DF与抛物线P相交于点N,则N的横坐标为
. 设射线DF与抛物线P相交于点N,则N的横坐标为%20.files/image298.gif) ,过N作x轴的垂线交x轴于H,有
,过N作x轴的垂线交x轴于H,有
点M不在抛物线P上,即点M不与N重合时,此时k的取值范围是
k≠%20.files/image304.gif) 且k>0.
且k>0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com