
题目列表(包括答案和解析)
已知函数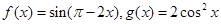 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
(A) 函数 在区间
在区间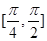 上为增函数
上为增函数
(B) 函数 的最小正周期为
的最小正周期为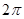
(C) 函数 的图象关于直线
的图象关于直线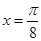 对称
对称
(D) 将函数 的图象向右平移
的图象向右平移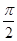 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数 的图象
的图象
(09年湖北补习学校联考文)下列命题正确的是 ( )
A.函数![]() 在区间
在区间![]() 内单调递增
内单调递增
B.函数![]() 的最小正周期为
的最小正周期为![]()
C.函数![]() 的图像是关于直线
的图像是关于直线![]() 成轴对称的图形
成轴对称的图形
D.函数![]() 的图像是关于点
的图像是关于点![]() 成中心对称的图形
成中心对称的图形
下列命题正确的是
A.函数![]() 在区间
在区间![]() 内单调递增
内单调递增
B.函数![]() 的最小正周期为
的最小正周期为![]()
C.函数![]() 的图像关于点
的图像关于点![]() 成中心对称
成中心对称
D.函数![]() 的图像关于直线
的图像关于直线![]() 成轴对称
成轴对称
(08年石家庄市一模文)设函数 ,则下列结论正确的是
,则下列结论正确的是
A.函数![]() 是奇函数 B.函数
是奇函数 B.函数![]() 的最小正周期为4
的最小正周期为4
C.函数![]() 在
在![]() 上为增函数 D.函数
上为增函数 D.函数![]() 无最小值
无最小值
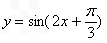 在区间
在区间 内单调递增
内单调递增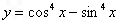 的最小正周期为
的最小正周期为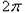
 的图像关于直线
的图像关于直线 成轴对称
成轴对称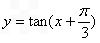 的图像关于点
的图像关于点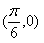 成中心对称
成中心对称一、选择题: B C A D B C A B D C
二、填空题:
11、 12、
12、 13、
13、
14、 15、②③
15、②③
三、解答题:
16.解:(1)  ……………………………1分
……………………………1分
 =
=
= =
= …………………………………………4分
…………………………………………4分
∵θ∈[π,2π],∴ ,
,
∴ ≤1 则
≤1 则  max=2
max=2 . ………………………………………………6分
. ………………………………………………6分
(2) 由已知 ,得
,得 …………………………………8分
…………………………………8分
又 ∴
∴ ……………………10分
……………………10分
∵θ∈[π,2π]∴ ,∴
,∴ . …………………12分
. …………………12分
17.解:依题意知: .……4分
.……4分
(1)对于
且 是奇函数……………………………………….……6分
是奇函数……………………………………….……6分
(2) 当
当 时,
时, 单调递减,
单调递减,
当 时,
时, 单调递增………………………………………….…8分
单调递增………………………………………….…8分
 ……….…………..…10分
……….…………..…10分
又 ………….……12分
………….……12分
18.解:(1)当
 ………………2分
………………2分

 ,..............................................5分
,..............................................5分
故 ................6分
................6分
定义域为 .................................7分
.................................7分
(2)对于 ,
,
显然当 (元), ..................................9分
(元), ..................................9分

∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多。..........12分
19.解:(1)由题意
 …………………………2分
…………………………2分
 当
当 时,
时, 取得极值,
取得极值,  所以
所以 

 即
即  …………………4分
…………………4分
此时当 时,
时, ,当
,当 时,
时, ,
,
 是函数
是函数 的最小值。
………………………6分
的最小值。
………………………6分
(2)设 ,则
,则  ,
, ……8分
……8分
设 ,
,
 ,令
,令 解得
解得 或
或
列表如下:











__
0
+










 函数
函数 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数。
上是减函数。
当 时,
时, 有极大值
有极大值 ;当
;当 时,
时, 有极小值
有极小值 ……10分
……10分
 函数
函数 与
与 的图象有两个公共点,
的图象有两个公共点, 函数
函数 与
与 的图象有两个公共点
的图象有两个公共点
 或
或 
 ……12分
……12分
20.解:(1)
 ,
,
 .令
.令 ,则
,则 .…………2分
.…………2分
 ,
, 当
当 时,
时, ,则
,则 .
. 数列
数列 不是等比数列.
不是等比数列.
 当
当 时,数列
时,数列 不是等比数列.………………… 5分
不是等比数列.………………… 5分
当 时,
时, ,则数列
,则数列 是等比数列,且公比为2.
是等比数列,且公比为2.
 ,即
,即 .解得
.解得 .……7分
.……7分
(2)由(Ⅰ)知,当 时,
时, ,
,
 .
.
令 , ………………………①
, ………………………①
则 , …………②
, …………②
由①-②:

 ,
,
 , ………………………………..………11分
, ………………………………..………11分
则
 . …………………..………13分
. …………………..………13分
21.解:(1)∵ 成等比数列 ∴
成等比数列 ∴
 设
设 是椭圆上任意一点,依椭圆的定义得
是椭圆上任意一点,依椭圆的定义得
即 为所求的椭圆方程.
……………………5分
为所求的椭圆方程.
……………………5分
(2)假设 存在,因
存在,因 与直线
与直线 相交,不可能垂直
相交,不可能垂直 轴 …………………6分
轴 …………………6分
因此可设 的方程为:
的方程为: 由
由

 ① ……………………8分
① ……………………8分
方程①有两个不等的实数根
∴ ② ………10分
② ………10分
设两个交点 、
、 的坐标分别为
的坐标分别为 ∴
∴
∵线段 恰被直线
恰被直线 平分 ∴
平分 ∴
∵ ∴
∴ ③ 把③代入②得
③ 把③代入②得 
∵ ∴
∴ ∴
∴ 解得
解得 或
或 ………13分
………13分
∴直线 的倾斜角范围为
的倾斜角范围为 …………………14分
…………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com