
题目列表(包括答案和解析)
已知函数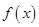 的定义域为
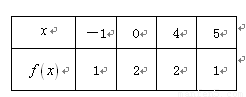
的定义域为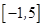 ,部分对应值如下表,
,部分对应值如下表,
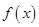 的导函数
的导函数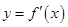 的图象如图所示.
的图象如图所示.
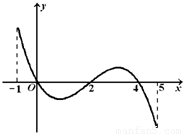
下列关于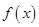 的命题:
的命题:
①函数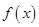 的极大值点为
的极大值点为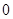 ,
,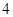 ;
;
②函数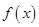 在
在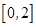 上是减函数;
上是减函数;
③如果当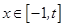 时,
时,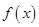 的最大值是2,那么
的最大值是2,那么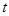 的最大值为4;
的最大值为4;
④函数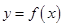 最多有2个零点.
最多有2个零点.
其中正确命题的序号是 ( )
A、①② B、③④ C、①②④ D、②③④.
已知两条直线![]() ,两个平面
,两个平面![]() ,给出下面四个命题:(C)
,给出下面四个命题:(C)
①![]() ②
②![]()
③![]() ④
④![]()
其中正确命题的序号是
A.①③ B.②④ C.①④ D.②③
设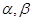 为互不重合的平面,
为互不重合的平面,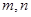 为互不重合的直线,给出下列四个命题:
为互不重合的直线,给出下列四个命题:
①若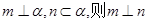 ; ②若
; ②若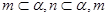 ∥
∥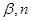 ∥
∥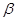 ,则
,则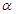 ∥
∥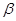 ;
;
③若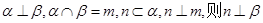 ;④若
;④若 .
.
其中正确命题的序号是 ( )
A.①和② B.①和③ C.②和④ D.③和④
给出下列命题
(1)实数的共轭复数一定是实数;
(2) 设复数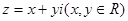 ,则满足
,则满足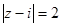 的复数
的复数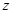 的轨迹是圆;
的轨迹是圆;
(3)若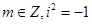 ,则
,则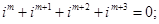
其中正确命题的序号是( )
A. 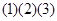 B.
B.
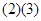 C.
C.
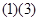 D.
D.
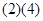
已知偶函数f(x)(x∈R),当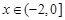 时,f(x)= -x(2+x),当
时,f(x)= -x(2+x),当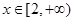 时,f(x)=(x-2)(a-x)(
时,f(x)=(x-2)(a-x)(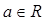 ).关于偶函数f(x)的图象G和直线
).关于偶函数f(x)的图象G和直线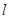 :y=m(
:y=m(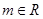 )的3个命题如下:
)的3个命题如下:
当a=2,m=0时,直线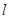 与图象G恰有3个公共点;
与图象G恰有3个公共点;
当a=3,m=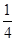 时,直线
时,直线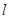 与图象G恰有6个公共点;
与图象G恰有6个公共点;
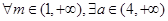 ,使得直线
,使得直线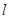 与图象G交于4个点,且相邻点之间的距离相等.其中正确命题的序号是(A)
与图象G交于4个点,且相邻点之间的距离相等.其中正确命题的序号是(A)
A. ①② B. ①③ C. ②③ D. ①②③
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
D
C
A
B
C
B
D
B
C
二、填空题:
13、 14、8 15、
14、8 15、 等; 16、7
等; 16、7
三、解答题
17、(1)由余弦定理: 又
又
∴ ∴
∴
(2)∵A+B+C= ∴
∴
∴
18、(1)周销售量为2吨,3吨,4吨的频率分别为0.2,0.5,和0.3。
(2) 可能的值为8,10,12,14,16
可能的值为8,10,12,14,16






8
10
12
14
16
P
0.04
0.2
0.37
0.3
0.09
则 的分布列为
的分布列为
∴ (千元)
(千元)
19、(1)AC=1,BC=2 ,AB= ,∴
,∴ ∴AC
∴AC
又 平面PAC 平面ABC,平面PAC
平面ABC,平面PAC 平面ABC=AC,∴BC
平面ABC=AC,∴BC 平面PAC
平面PAC
又∵PA 平面APC ∴
平面APC ∴
 (2)该几何体的主试图如下:
(2)该几何体的主试图如下:
几何体主试图的面积为
 ∴
∴ ∴
∴
(3)取PC 的中点N,连接AN,由△PAC是边长为1的正三角形,可知
由(1)BC 平面PAC,可知
平面PAC,可知 ∴
∴ 平面PCBM
平面PCBM
∴
20、(1)要使得不等式 能成立,只需
能成立,只需
 ∴
∴
∴ ,故实数m的最小值为1
,故实数m的最小值为1
(2)由 得
得
令 ∵
∵ ,列表如下:
,列表如下:
x
0
(0,1)
1
(1,2)
2


0


1
减函数

增函数
3-2ln3
∴
21、(1)曲线C的方程为
(2) ,存在点M(―1,2)满足题意
,存在点M(―1,2)满足题意
22、(1)由于点B1(1,y1),B2(2,y2),…,Bn(n,yn)( )在直线
)在直线 上
上
则 因此
因此 ,所以
,所以 是等差数列
是等差数列
(2)由已知有 得
得 同理
同理 
∴
∴

∴
(3)由(2)得 ,则
,则

∴
∴
∴
由于 而
而
则
 ,从而
,从而
同理: ……
…… 
以上 个不等式相加得:
个不等式相加得:
即 ,从而
,从而

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com