
题目列表(包括答案和解析)
下列命题中正确的个数是( ).
(1)若直线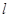 上有无数个点不在平面
上有无数个点不在平面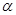 内,则
内,则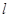 ∥
∥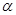 .
.
(2)若直线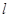 与平面
与平面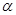 平行,则
平行,则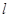 与平面
与平面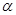 内的任意一条直线都平行.
内的任意一条直线都平行.
(3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.
(4)若直线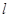 与平面
与平面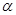 平行,则
平行,则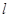 与平面
与平面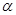 内的任意一条直线都没有公共点.
内的任意一条直线都没有公共点.
A.0 B. 1 C. 2 D.3
现给出如下命题:
(1)若直线与平面内无穷多条直线都垂直,则直线;
(2)空间三点确定一个平面;
(3) 先后抛两枚硬币,用事件A表示“第一次抛出现正面向上”,用事件B表示“第二次抛出现反面向上”,则事件A和B相互独立且=;
(4)样本数据的标准差是1.
则其中正确命题的序号是 [答]( )
A.(1)、(4). B.(1)、(3). C.(2)、(3)、(4). D.(3)、(4).
现给出如下命题:
(1)若直线![]() 与平面
与平面![]() 内无穷多条直线都垂直,则直线
内无穷多条直线都垂直,则直线![]() ;
;
(2)已知![]() ,则
,则![]() ;
;
(3)某种乐器发出的声波可用函数![]() 来描述,则该声波的频率是200赫兹;
来描述,则该声波的频率是200赫兹;
(4)样本数据![]() 的标准差是1.
的标准差是1.
则其中正确命题的序号是 [答]( )
A.(1)、(4). B.(1)、(3). C.(2)、(3)、(4). D.(3)、(4).
现给出如下命题:
(1)若直线与平面内无穷多条直线都垂直,则直线;
(2)空间三点确定一个平面;
(3) 先后抛两枚硬币,用事件A表示“第一次抛出现正面向上”,用事件B表示“第二次抛出现反面向上”,则事件A和B相互独立且=;
(4)样本数据的标准差是1.
则其中正确命题的序号是 [答]( )
A.(1)、(4). B.(1)、(3). C.(2)、(3)、(4). D.(3)、(4).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com