题目列表(包括答案和解析)
函数f(x)在定义域R内可导，若f(x)＝f(2－x)，且当x∈(－∞，1)时，(x－1)f′(x)<0，设a＝f(0)，b＝f(
)，c＝f(3)，则 ( )
A．a<b<c B．c<a<b
C．c<b<a D．b<c<a
已知定义在R上的函数y=f(x)满足以下三个条件：
(1)对任意的x∈R，都有f(x+4)=f(x);
(2)对任意的x1，x2∈R，且0≤x1<x2≤2,都有f(x1)<f(x2);
(3)函数y=f(x+2)的图像关于y轴对称.
则a=f(4.5)，b=f(6.5),c=f(7)从小到大的关系是_____
设函数f(x)＝x2－4x＋3，g(x)＝3x－2，集合M＝{x∈R|f(g(x))>0}，N＝{x∈R|g(x)<2}，则M∩N为 ( )
A．(1，＋∞) B．(0,1)
C．(－1,1) D．(－∞，1)
已知映射f：A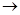
B, A=B=R,对应法则f：x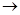y
= –x2+2x,对于实数k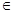
B在A中没有原象，则k的取值范围是
（ ）
A．k>1 B．k≥1 C．k<1 D．k≤2
一批零件共10个，其中有8个合格品，2个次品，每次任取一个零件装配机器，若第2
次取到的是合格品的概率为P2，第3次取到的是合格品的概率为P3，则 （ ）
A．P2> P3 B．P2= P3
C．P2< P3 D．P2与P3的大小不能确定
一、选择题（60分）
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
C
B
（C
D
D
A
B
C
B
二、填空题（20分）
13. 15 14．5 15． 
16． 
三、解答题（70分）
17．（1）
，∴
，∴
（5分）
（2）
∵
，∴
，∴
∴
（理10分）
18．
（1）记“甲恰好投进两球”为事件A，则
（6分）
（2）记“甲比乙多投进两球”，其中“恰好甲投进两球且乙未投进”为事件
，“恰好甲投进三球且乙投进一球”为事件
，根据提议，、互斥，
（理12分）
19．（1） （6分）
（2） （文12分）
（3） （理12分）
20．（1）设数列
的公比为
，则
∴
则
（文6分，理4分）
（2）由（1）可知
所以数列
是一个以
为首项，1为公差的等差数列
∴
（文12分，理8分）
（3）∵
∴当
时，
，即
当
时，
，即
综上可知：时，；时， （理12分）
21. ⑴由已知
所求双曲线C的方程为
;
⑵设P点的坐标为
,M,N的纵坐标分别为
.
共线
同理
22．
（1）由题意得：
∴在
上
；在
上
；在
上
在此
在
处取得极小值
∴
①
②
③
由①②③联立得：
∴
（6分）
（2）设切点Q
过
令
，
求得：
，方程
有三个根。
需：
故：
因此所求实数
的取值范围为：
（理12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com