练习册

  • 练习册
  • 试题
    设M是由满足下列条件的函数构成的集合:“①方程有实数根, 【查看更多】

     

    题目列表(包括答案和解析)

    设M是由满足下列条件的函数构成的集合：“①方程有实数根；②函数的导数满足.”

    （1）判断函数是否是集合M中的元素，并说明理由；

    （2）集合M中的元素具有下面的性质：若的定义域为D，则对于任意，都存在，使得等式成立”，试用这一性质证明：方程只有一个实数根；

    （3）设是方程的实数根，求证：对于定义域中任意的，当，且时，.

    查看答案和解析>>

    设M是由满足下列条件的函数构成的集合：“①方程有实数根；②函数的导数满足.”

       （I）判断函数是否是集合M中的元素，并说明理由；

       （II）集合M中的元素具有下面的性质：若的定义域为D，则对于任意

    [m，n]D，都存在[m，n]，使得等式成立”，

    试用这一性质证明：方程只有一个实数根；

       （III）设是方程的实数根，求证：对于定义域中任意的.

    查看答案和解析>>

    设M是由满足下列条件的函数构成的集合：①方程，有实数根②函数的导数满足.

    (I) 若函数为集合M中的任意一个元素，证明：方程只有一个实数根；

    (II) 判断函数是否是集合M中的元素,并说明理由；

    (III) 设函数为集合M中的任意一个元素，对于定义域中任意，当,且时,证明：.

     

    查看答案和解析>>

    设M是由满足下列条件的函数构成的集合：“①方程有实数

    根；②函数”[来源:学+科+网Z+X+X+K]

    （I）判断函数是否是集合M中的元素，并说明理由；

    （II）集合M中的元素具有下面的性质：若 的定义域为D，则对于任意

    成立。试用这一性

    质证明：方程只有一个实数根；

    （III）对于M中的函数 的实数根，求证：对于定义

    域中任意的当且

     

    查看答案和解析>>

    设M是由满足下列条件的函数构成的集合：①方程，有实数根②函数的导数满足.
    (I) 若函数为集合M中的任意一个元素，证明：方程只有一个实数根；
    (II) 判断函数是否是集合M中的元素,并说明理由；
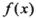    (III) 设函数为集合M中的任意一个元素，对于定义域中任意，当,且时,证明：.

    查看答案和解析>>

     

    一、选择题（本大题共8小题，每小题5分，共40分）

    1―5  CACBB        6―8  DDA

    二、填空题（本大题共6小题，每小题5分，共30分）

    9．                           10．

    11．                         12．

    13．                      14．

    三、解答题：本大题共6小题共80-分。解答题应写出文字说明，证明过程或演算步骤。

    15．（本小题共满分13分）

    解：（I）由图知：，得A=2；

        由A+B=3，得B=1；

       

        设

    将函数的图象向左平移，得

    的图象，

    则

                              ……………………8分

       （II）依题意：

    当

    此时x的取值集合为   …………………………13分

       （I）证明：取AC中点F，连结MF，BF，

    在三角形AC1C中，MN//C1C且

    ，

           

       （II）设A1到平面AB1C1的距离为h，AA1⊥平面A1B1C1

           

       （III）三棱柱ABC―A1B1C1是直三棱柱，平面ABB1A1⊥平面A1B1C1，又点D是等腰直角三角形A1B1C1斜边A1B1的中点。

    则C1D⊥A1B1

    所以，；

    平面A1B1BA内，过D作DE⊥AB1，垂足为E，连结C1E，则C1E⊥AB1；

    是二面角，A1―AB1―C1的平面角，

    在Rt

     

    所以，二面角，A1―AB1―C1的大小为   ………………14分

    17．（本小题满分13分）

    解：（I）设在第一次更换灯棍工作中，不需要更换灯棍的概率为P1，则

                                           ………………………………4分

       （II）对该盏灯来说，在第1，2次都更换了灯棍的概率为；在第一次未更换灯棍而在第二次需要更换灯棍的概率为，故所求概率为

              ………………………………8分

       （III）的可能取值为0，1，2，3；

        某盏灯在第二次灯棍更换工作中需要更换灯棍的概率为

       

        的分布列为

       

    P

    0

    1

    2

    3

        此分布为二项分布―N（3，0.6）

                                …………………………13分

    18．（本小题满分13分）

        解：

       

        设M（m，4-m2），则过M点曲线C的切线斜率k=-2m。

                  …………………………6分

        由x=0，得

        由y=0，得

        设△AOB的面积为S，则

       

        令

        当上为减函数；

        当上为增函数；

        …………13分

    19．（本小题满分14分）

       （I）由焦点F（1，0）在上，得……………………1分

    设点N（m，n）则 有：，      …………………………3分

    解得，                       ……………………5分

    N点不在抛物线C上。                    ………………………………7分

       （2）把直线方程代入抛物线方程得：

    解得。………………12分

    当P与M重合时，a=1

    20．（本小题满分13分）

        解：（I）因为，又因为当x=0时，f（0）=0，所以方程f（x）-x=0有实数根0。

        所以函数是的集合M中的元素。………………………………3分

       （II）假设方程f（x）-x=0存在两个实数根不妨设，根据题意存在数

            使得等式成立。

            因为

            与已知矛盾，所以方程只有一个实数根；…………8分

       （III）不妨设

        又因为为减函数，

    所以

    所以

        所以

             …………………………13分

     


    同步练习册答案