
题目列表(包括答案和解析)
设抛物线y2=4x截直线y=2x+k所得弦长|AB|=3![]() .
.
(1)求k的值;
(2)以弦AB为底边,x轴上的P点为顶点组成的三角形面积为39时,求点P的坐标.
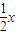 相交,所得弦长为2.
相交,所得弦长为2. ,sin(α-β)=
,sin(α-β)= ,则tanαcotβ=5.
,则tanαcotβ=5.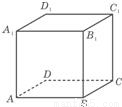
(1)求k的值;
(2)以弦AB为底边,x轴上的P点为顶点组成的三角形面积为39时,求点P的坐标.
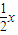 相交,所得弦长为2.
相交,所得弦长为2. ,sin(α-β)=
,sin(α-β)= ,则tanαcotβ=5.
,则tanαcotβ=5.
①将函数y=|x+1|的图象按向量v=(-1,0)平移,得到的图象对应的函数表达式为y=|x|;
②圆x2+y2+4x-2y+1=0与直线y=![]() 相交,所得弦长为2;
相交,所得弦长为2;
③若sin(α+β)=![]() ,sin(α-β)=
,sin(α-β)=![]() ,则tanαcotβ=5;
,则tanαcotβ=5;

④如图,已知正方体ABCD-A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com