
题目列表(包括答案和解析)
(08年潍坊市质检)(14分)已知向量m=(a,-x),n=(ln(1+ex),a+1),![]() = m?n,
= m?n,![]() 且
且![]() 在x=1处取得极值.
在x=1处取得极值.
(1)求a的值,并判断![]() 的单调性;
的单调性;
(2)当![]() ;
;
(3)设△ABC的三个顶点A、B、C都在![]() 图象上,横坐标依次成等差数列,证明:△ABC为钝角三角形,并判断是否可能是等腰三角形,说明理由.
图象上,横坐标依次成等差数列,证明:△ABC为钝角三角形,并判断是否可能是等腰三角形,说明理由.
设函数f(x)= 在[1,+∞
在[1,+∞ 上为增函数.
上为增函数.
(1)求正实数a的取值范围;
(2)比较 的大小,说明理由;
的大小,说明理由;
(3)求证: (n∈N*, n≥2)
(n∈N*, n≥2)
【解析】第一问中,利用
解:(1)由已知: ,依题意得:
,依题意得: ≥0对x∈[1,+∞
≥0对x∈[1,+∞ 恒成立
恒成立
∴ax-1≥0对x∈[1,+∞ 恒成立 ∴a-1≥0即:a≥1
恒成立 ∴a-1≥0即:a≥1
(2)∵a=1 ∴由(1)知:f(x)= 在[1,+∞)上为增函数,
在[1,+∞)上为增函数,
∴n≥2时:f( )=
)=
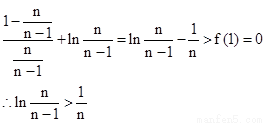
(3) ∵ ∴
∴
 (其中常数λ>0,n∈N*).
(其中常数λ>0,n∈N*).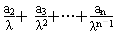 =n2+2n(其中常数λ>0,n∈N*),
=n2+2n(其中常数λ>0,n∈N*),已知数列{an}满足:a1++ +…+=n2+2n(其中常数λ>0,n∈N*).
(1)求数列{an}的通项公式;
(2)当λ=4时,是否存在互不相同的正整数r,s,t,使得ar,as,at成等比数列?若存在,给出r,s,t满足的条件;若不存在,说明理由;
(3)设Sn为数列{an}的前n项和.若对任意n∈N*,都有(1-λ)Sn+λan≥2λn恒成立,求实数λ的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com