
题目列表(包括答案和解析)
解::因为![]() ,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=
,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=![]() 与y=-
与y=-![]() 在(0,+
在(0,+![]() )上都是增函数,因此
)上都是增函数,因此![]() 在(0,+
在(0,+![]() )上是增函数,所以零点个数只有一个方法2:把函数
)上是增函数,所以零点个数只有一个方法2:把函数![]() 的零点个数个数问题转化为判断方程
的零点个数个数问题转化为判断方程![]() 解的个数问题,近而转化成判断
解的个数问题,近而转化成判断![]() 与
与![]() 交点个数问题,在坐标系中画出图形
交点个数问题,在坐标系中画出图形
由图看出显然一个交点,因此函数![]() 的零点个数只有一个
的零点个数只有一个
袋中有50个大小相同的号牌,其中标着0号的有5个,标着n号的有n个(n=1,2,…9),现从袋中任取一球,求所取号码的分布列,以及取得号码为偶数的概率.
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列” ,将构图边数增加到
,将构图边数增加到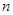 可得到“
可得到“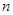 边形数列”,记它的第
边形数列”,记它的第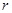 项为
项为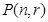 ,
,
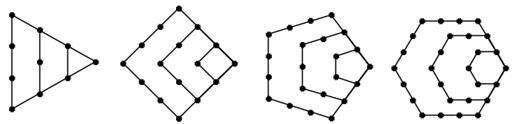
1,3,6,10 1,4,9,16 1,5,12,22 1,6,15,28
(1)
求使得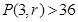 的最小
的最小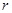 的取值;
的取值;
(2)
试推导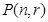 关于
关于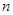 、
、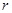 的解析式;
的解析式;
( 3) 是否存在这样的“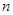 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
 ,将构图边数增加到
,将构图边数增加到 可得到“
可得到“ 边形数列”,记它的第
边形数列”,记它的第 项为
项为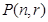 ,
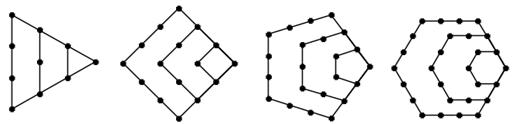
,
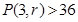 的最小
的最小 的取值;
的取值;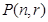 关于
关于 、
、 的解析式;
的解析式; 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.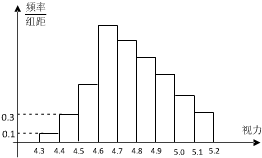 为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a+b的值为
为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a+b的值为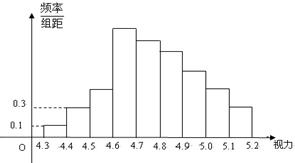 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图所示;由于不慎将部分数据丢失,但知道前4组的频数从左到右依次是等比数列{an}的前四项,后6组的频数从左到右依次是等差数列{bn}的前六项.
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图所示;由于不慎将部分数据丢失,但知道前4组的频数从左到右依次是等比数列{an}的前四项,后6组的频数从左到右依次是等差数列{bn}的前六项.| c1 |
| a1 |
| c2 |
| a2 |
| cn |
| an |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com