练习册

  • 练习册
  • 试题
    22． 证明不等式: 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分14分）已知在函数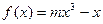的图象上以N（1，n）为切点的切线的倾斜角为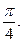
    （1）求m、n的值；
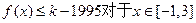             （2）是否存在最小的正整数k，使得不等式恒成立？如果存在，请求出最小的正整数k；如果不存在，请说明理由；
    （3）求证：.

    查看答案和解析>>

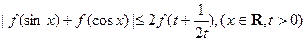    （本小题满分14分）
    有个首项都是1的等差数列，设第个数列的第项为，公差为，并且成等差数列．
    （Ⅰ）证明（，是的多项式），并求的值
    （Ⅱ）当时，将数列分组如下：
    (每组数的个数构成等差数列)．
    设前组中所有数之和为，求数列的前项和．
    （Ⅲ）设是不超过20的正整数，当时，对于（Ⅱ）中的，求使得不等式
    成立的所有的值．

    查看答案和解析>>

    （本小题满分14分）已知各项均不为零的数列{an}的前n项和为Sn，且满足a1＝c，
    2Sn＝an an＋1＋r．
    （1）若r＝－6，数列{an}能否成为等差数列？若能，求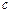满足的条件；若不能，请说明理由；
    （2）设，，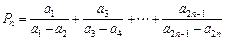
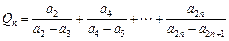    若r＞c＞4，求证：对于一切n∈N*，不等式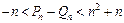恒成立．

    查看答案和解析>>

    （本小题满分14分）
    已知函数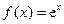（为自然对数的底数），，,．
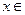
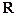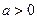    （1）判断函数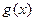的奇偶性,并说明理由；
    （2）求函数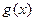的单调递增区间；
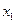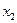    （3）证明：对任意实数和，且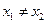，都有不等式
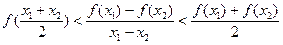    成立．

    查看答案和解析>>

    （本小题满分14分）本题（1）、（2）、（3）三个选答题，每小题7分，任选2题作答，满分14分，如果多做，则按所做的前两题计分。作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。
    （1）(本小题满分7分) 选修4-2:矩阵与变换
    已知，若所对应的变换把直线变换为自身，求实数，并求的逆矩阵。
    （2）（本题满分7分）选修4-4：坐标系与参数方程
    已知直线的参数方程：（为参数）和圆的极坐标方程：。
    ①将直线的参数方程化为普通方程，圆的极坐标方程化为直角坐标方程；
    ②判断直线和圆的位置关系。
    （3）（本题满分7分）选修4-5：不等式选讲
    已知函数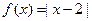
    ①解不等式；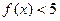
    ②证明：对任意，不等式成立.

    查看答案和解析>>

     

    一、选择题

    A卷：BACDB    DCABD    BA

    B卷：BDACD    BDCAB    BA

    二、填空题

    13．15  

    14．210

    15．

    16．①④

    三、解答题：

    17． 解：（注：考试中计算此题可以使用分数，以下的解答用的是小数）

       （Ⅰ）同文（Ⅰ）

       （Ⅱ）的概率分别为

    随机变量的概率分布为

    0

    1

    2

    3

    P

    0.216

    0.432

    0.288

    0.064

    ………………8分

    的数学期望为E=0×0.216+1×0.432+2×0.288+3×0.064=1.2.…………10分

    （或利用E=mp=3×0.4=1.2）

    的方差为

    D=（0－1.2）2×0.216+（1－1.2）2×0.432+（2－1.2）2×0.288+（3－1.2）2×0.064

    =0.72.…………………………12分

    （或利用D=nq=3×0.4×0.6=0.72）

     

    18．解：

       （Ⅰ）

    …………4分

    所以，的最小正周期，最小值为－2.…………………………6分

       （Ⅱ）列表：

    x

    0

    2

    0

    －2

    0

     

     

     

     

     

     

     

     

     

     

     

     

    …………………12分

    （19?文）同18?理.

    （19?理）解：（Ⅰ）取A1A的中点P，连PM、PN，则PN//AD，

    …………………………6分

     

     

     

     

     

     

     

     

     

     

     

     

       （Ⅱ）由（Ⅰ）知，则就是所求二面角的平面角.………………………8分

             显然

    利用等面积法求得A1O=AO=在△A1OA中由余弦定理得

    cos∠A1OA=.

    所以二面角的大小为arccos……………………………………………12分

    （20?文）同19理.

    （20?理）（I）证明：当q>0时，由a1>0，知an>0，所以Sn>0；………………2分

    当－1<q<0时，因为a1>0，1－q>0，1－qn>0，所以.

    综上，当q>－1且q≠0时，Sn>0总成立.……………………5分

       （II）解：an+1=anq，an+2=anq2，所以bn=an+1－kan+2=an(q－kq2).

            Tn=b1+b2+…+bn=(a1+a2+…+an)(q－kq2)=Sn(q－kq2).……………………9分

            依题意，由Tn>kSn，得Sn(q－kq2)>kSn.

            ∵Sn>0，∴可得q－kq2>k，

    即k(1+q2)<q，k<.

    ∵

    ∴k的取值范围是. ……………………12分

    （21?文）解：f′(x)=3x2+4ax－b.………………………………2分

             设f′(x)=0的二根为x1，x2，由已知得

             x1=－1，x2≥2，………………………………………………4分

             …………………………7分

            解得

            故a的取值范围是…………………………………………12分

    （21?理）解：（I）设椭圆方程

            由2c=4得c=2，又.

            故a=3，b2=a2－c2=5，

            ∴所求的椭圆方程.…………………………………………5分

       （II）点F的坐标为（0，2），设直线AB的方程为y=kx+2,A(x1,y1)、B(x2，y2).

    由得(9+5k2)x2+20kx－25=0，………………………………8分

    显然△>0成立，

    根据韦达定理得

    ，                       ①

    .                           ②

    ,

    ,代入①、②得

                                         ③

                                        ④

    由③、④得

     …………………………………………14分

    （22．文）同21理，其中3分、6分、8分、12分依次更改为5分、8分、10分、14分.

    （22．理）（1）证明：令

    原不等式…………………………2分

    令，

    单调递增，，

    ………………………………………………5分

    令，

    单调递增，，

     …………………………………………8分

    ………………………………9分

       （Ⅱ）令，上式也成立

    将各式相加

    ……………11分

    即

    ……………………………………………………………………14分

     


    同步练习册答案