
题目列表(包括答案和解析)

 之间的等量关系式,并充分说明理由。
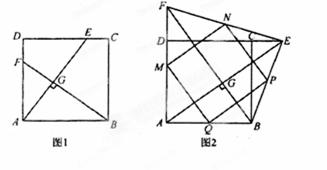
之间的等量关系式,并充分说明理由。 如图1,正方形ABCD中,点E、F分别在边DC、AD上,且AE⊥BF于G.
(1)求证:BF=AE
(2)如图2,当点E在DC延长线上,点F在AD延长线上时,(1)中结论是否成立(直接写结论)
(3)在图2中,若点M、N、P、Q分别为四边形AFEB四条边AF、EF、EB、AB的中点,且AF:AD=4:3,求S四边形MNPQ: S正方形ABCD(本小题10分)
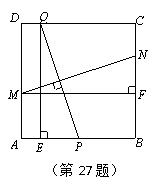
(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
 |
(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
 |
(本题满分8分)如图,在正方形ABCD中,E是AB边上任意一点,BG⊥CE,垂足为点O,交AC于点F,交AD于点G。
(1)证明:BE=AG ;
(2)点E位于什么位置时,∠AEF=∠CEB,说明理由。
一、选择题:
题号
1
2
3
4
5
6
7
8
答案
C
D
B
B
B
D
C
B
二、填空题:
9. x≥ ,10. ,11. 6 ,12. ,13. 5 ,14. 2.5 ,
15. 161 , 16. (-b,a) ,17. -5 ,18. 6π 。
三、解答题
19. 20. ,求值略 21. -2<x≤3,1,2,3
22.解:(1)∵四边形ABCD是正方形
∴∠ABC=90°, ∴∠1+∠3=90°
∵BG⊥CE ∠BOC=90°
∴∠2+∠3=90° ∴∠1=∠2
在ㄓGAB和ㄓEBC中,
∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2
∴ㄓGAB≌ㄓEBC(ASA) ∴AG=BE
(2)当点E位于线段AB中点时,∠AEF=∠CEB。理由如下:
当点E位于线段AB中点时,AE=BE
由(1)知,AG=BE ∴AG=AE
∵四边形ABCD是正方形 ∴∠GAF=∠EAF=45°
又∵AF=AF ∴ㄓGAF≌ㄓEAF(SAS)∴∠AGF=∠AEF
由(1)知,ㄓGAB≌ㄓEBC ∴∠AGF=∠CEB ∴∠AEF=∠CEB
23.(1)略(2)一共抽查了500 名学生,三姿良好的学生约有12000 人;
(3)看法:只要点评具有正确的导向性,且符合以下要点的意思,均可给分
要点: 中学生应该坚持锻炼身体,努力纠正坐姿、站姿、走姿中的不良习惯,促进身心健康发育。
25.(1)4.5米.(2)7.9米
如图,延长AG交BE于N点,GM⊥BE,
则有MN=DE=4
因为AB的影长BN=6.5+4=10.5
所以AB长约为7.9米
26.(1)y=-x+130
(2)ω=(x-50)(130-x)=-(x-90)2+1600
但是50≤x≤75,且在此范围内ω随x增大而增大,所以当x=75时,ω最大
当x=75时,ω最大值为1375元
27.(1) (2)A1(0,5),B1(2,1) (3)M(0,)
28.(1)15 (2)当0≤x≤4时,y=-x2+5x ; 当4<x≤10时,y=-2x+24
当y=10时,x=7或x=
(3)当4≤y<16时,平移的距离不等,两纸片重叠的面积可能相等;
0≤y<4或y=16时,平移的距离不等,两纸片重叠部分的面积也不可能相等
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com