
题目列表(包括答案和解析)
(本小题满分13分)
在△ABC中,a,b,c分别为内角A,B,C所对的边长,a=![]() ,b=
,b=![]() ,
,![]() ,求边BC上的高.
,求边BC上的高.
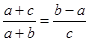 ,
,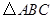 最大边的边长为
最大边的边长为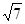 ,且
,且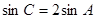 ,求最小边长.
,求最小边长.(本小题满分13分)
在锐角△ABC中,角A、B、C所对的边分别为a、b、c,已知![]()
(1)求![]() 的值;
的值;
(2)若![]()
(本小题满分13分)
如图在直三棱柱ABC—A1B1C1中,AC=BC=2,AA1=![]() ,∠ACB=90°,M是AA1的中点,N是BC1的中点。
,∠ACB=90°,M是AA1的中点,N是BC1的中点。
(1)求证:MN∥平面A1B1C1
|
(3)求二面角B-C1M—A的大小.
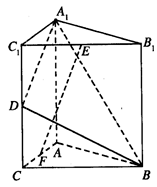 (本小题满分13分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(本小题满分13分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求二面角B—A1D—A的平面角余弦值;
(2)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
若存在,确定其位置并证明结论;若不存在,说明理由.
一、选择题
1―8 DAACA CBD
二、填空题
9. 10.
10. 11.
11. 12.
12. 13.50 14.5
13.50 14.5
三、解答题
15.(本小题满分13分)
解:(1)由 ………………2分
………………2分
整理得
即 ……………………3分
……………………3分
又 ……………………5分
……………………5分
又因为 ,
,
所以 …………………………6分
…………………………6分
(2)因为 ,所以
,所以
故 …………………………7分
…………………………7分
由
即 ,
,
所以 .
.
即 .……………………11分
.……………………11分
因为 ……………………12分
……………………12分
故
所以 ……………………13分
……………………13分
16.(本小题满分13分)
解:(1)取AC的中点O,连结OS,OB。
∵SA=SC,AB=BC,
∴AC⊥SO,AC⊥OB。又平面SAC⊥平面ABC,且平面SAC∩平面ABC=BC,
∴SO⊥平面ABC。
故SB在平面ABC内的射影为OB。
∴AC⊥SB.……………………6分
(2)取OB的中点D,作NE⊥CM交GM于E,连结DE,ND。
在△SOB中,N、D分别为SB,OB的中点,
∴DN//SO,又SO⊥平面ABC,
∴DN⊥平面ABC,由NE⊥CM得DE⊥CM。
故∠NED为二面角N―CM―B的平面角,………………9分
设OB与CM交于G,则G为△ABC的中心
∴ DE⊥CM,BM⊥CM,
DE⊥CM,BM⊥CM,
|