
题目列表(包括答案和解析)
(本小题满分12分)
在交通拥挤地段,为了确保交通安全,规定机动车相互之间的距离d(米)与车速v(千米/小时)需遵循的关系是d≥ (其中a(米)是车身长,a为常量),同时规定d≥
(其中a(米)是车身长,a为常量),同时规定d≥ .
.
(1)当d= 时,求机动车车速的变化范围;
时,求机动车车速的变化范围;
(2)设机动车每小时流量Q= ,应规定怎样的车速,使机动车每小时流量Q最大.
,应规定怎样的车速,使机动车每小时流量Q最大.
设椭圆 (常数
(常数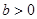 )的左右焦点分别为
)的左右焦点分别为 ,
, 是直线
是直线 上的两个动点,
上的两个动点, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一问中解:设 ,
, 则
则
由 得
得 由
由 ,得
,得
 ②
②

第二问易求椭圆 的标准方程为:
的标准方程为:
 ,
,
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .
.
解:设 ,
, ……………………1分
……………………1分
则 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求椭圆 的标准方程为:
的标准方程为: .………………2分
.………………2分
 , ……4分
, ……4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值
| 4x+a |
| x2+1 |
| 12 |
| 5 |
| 12 |
| 25 |
| 2 |
| x |
| 8 |
| 5 |
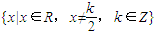 ,且f(x)+f(2-x)=0,
,且f(x)+f(2-x)=0, ,当
,当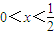 时,f(x)=3x.
时,f(x)=3x.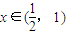 时函数f(x)的解析式,并求x∈
时函数f(x)的解析式,并求x∈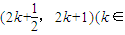 Z)时f(x)的解析式;
Z)时f(x)的解析式;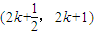 时,解不等式log3f(x)>x2-(2k+2)x+2k+1.
时,解不等式log3f(x)>x2-(2k+2)x+2k+1.、已知函数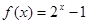 的反函数为
的反函数为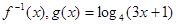
(1)若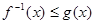 ,求
,求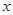 的取值范围D;
的取值范围D;
(2)设函数 ;当
;当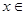 D时,求函数H
D时,求函数H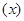 的值域
的值域
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com