
题目列表(包括答案和解析)
已知函数
(1) 若函数 在
在 上单调,求
上单调,求 的值;
的值;
(2)若函数 在区间
在区间 上的最大值是
上的最大值是 ,求
,求 的取值范围.
的取值范围.
【解析】第一问,

 ,
,  、
、
第二问中,
由(1)知: 当 时,
时,  上单调递增
上单调递增

 满足条件当
满足条件当 时,
时, 
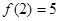


解: (1) 
 ……3分
……3分
 ,
,  …………….7分
…………….7分
(2) 
由(1)知: 当 时,
时,  上单调递增
上单调递增

 满足条件…………..10分
满足条件…………..10分
当 时,
时,  且
且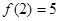

 …………13分
…………13分
综上所述: 
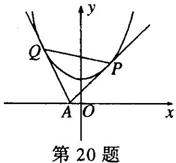
(09年湖北八校联考文)(13分)过![]() 轴上动点
轴上动点![]() 引抛物线
引抛物线![]() 的两条切线
的两条切线![]() ,
,![]() ,
,![]() ,
,![]() 为切点.
为切点.
(Ⅰ)若切线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() 和
和![]() ,求证:
,求证:![]() 为定值,并求出定值.
为定值,并求出定值.
(Ⅱ) 求证:直线![]() 恒过定点,并求出定点坐标.
恒过定点,并求出定点坐标.
(Ⅲ)当![]() 最小时,求
最小时,求![]() 的值.
的值.
(本小题满分13分)
设 .
.
(1)如果 在
在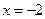 处取得最小值
处取得最小值 ,求
,求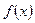 的解析式;
的解析式;
(2)如果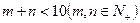 ,
,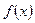 的单调递减区间的长度是正整数,试求
的单调递减区间的长度是正整数,试求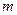 和
和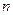
的值.(注:区间 的长度为
的长度为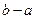 )
)
(09年湖南师大附中月考理)(13分)
已知![]()
![]() ,
,![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,且满足
的等比数列,且满足![]() 。
。
(1)求![]() 的值。
的值。
(2)数列![]() 与数列
与数列![]() 有公共项,且公共项按原顺序排列后构成一个新数列
有公共项,且公共项按原顺序排列后构成一个新数列![]() ,求
,求![]() 的通项。
的通项。
(3)记(2)中![]() 的前
的前![]() 项之和
项之和![]() ,对于不小于3的正整数
,对于不小于3的正整数![]() ,求证:
,求证:
(09年湖南师大附中月考理)(13分)
某加工厂需定期购买原材料,已知每公斤原材料的价格为1.5元,每次购买原材料需支付运费600元,每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管)。
(1)设该厂每![]() 天购买一次原材料,试写出每次购买的原材料在
天购买一次原材料,试写出每次购买的原材料在![]() 天内总的保管费用
天内总的保管费用![]() 关于
关于![]() 的函数关系式;
的函数关系式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com