
题目列表(包括答案和解析)
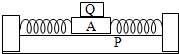 某同学设计了一个测量物体质量的装置,如图所示,其中P是光滑水平面,A是质量为M的带夹子的已知质量金属块,Q是待测质量的物体(可以被A上的夹子固定).已知该装置的弹簧振子做简谐运动的周期为
某同学设计了一个测量物体质量的装置,如图所示,其中P是光滑水平面,A是质量为M的带夹子的已知质量金属块,Q是待测质量的物体(可以被A上的夹子固定).已知该装置的弹簧振子做简谐运动的周期为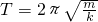 (数量级为100s),其中m是振子的质量,K是与弹簧的劲度系数有关的常数.
(数量级为100s),其中m是振子的质量,K是与弹簧的劲度系数有关的常数.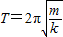 (数量级为10s),其中m是振子的质量,K是与弹簧的劲度系数有关的常数.
(数量级为10s),其中m是振子的质量,K是与弹簧的劲度系数有关的常数.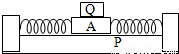
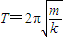 (数量级为10s),其中m是振子的质量,K是与弹簧的劲度系数有关的常数.
(数量级为10s),其中m是振子的质量,K是与弹簧的劲度系数有关的常数.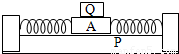
![]() 一根长为约30cm、管内载面积为S=5.0×10-6m2的玻璃管下端有一个球形小容器,管内有一段长约1cm的水银柱.现在需要用比较准确的方法测定球形小容器的容积V.可用的器材有:刻度尺(量程500mm)、温度计(测量范围0-100℃)、玻璃容器(高约30cm,直径约10cm)、足够多的沸水和冷水.
一根长为约30cm、管内载面积为S=5.0×10-6m2的玻璃管下端有一个球形小容器,管内有一段长约1cm的水银柱.现在需要用比较准确的方法测定球形小容器的容积V.可用的器材有:刻度尺(量程500mm)、温度计(测量范围0-100℃)、玻璃容器(高约30cm,直径约10cm)、足够多的沸水和冷水.
(1)简要写出实验步骤及需要测量的物理量;
(2)说明如何根据所测得的物理量得出实验结果.
13
14
15
16
17
18
19
20
A
A
B
C
D
A
B
D
21、(每空3分,即每小题6分,共18分)
(1)(9分)
① A、不放Q时用秒表测出振子振动20次的时间t1,(或测出振子的周期T1),
B、将Q固定在A上,用秒表测出振子振动20次的时间t2,(或测出振子的周期T2)
②/09石景山二模物理部分(纯WORD版).files/image036.gif) 或
或/09石景山二模物理部分(纯WORD版).files/image038.gif)
(3)①0.5,2,8,18,32 ②2ω2
③/09石景山二模物理部分(纯WORD版).files/image040.gif)
22.(16分)
解:(1)8m/s, (2)3.3m
23.(18分)
解:(1)1.6N, (2)0.25C
24.(20分)
解:(1)依题意,R=L/4,由qvB=mv2/R,qU0=/09石景山二模物理部分(纯WORD版).files/image042.gif) ,解得U0=
,解得U0=/09石景山二模物理部分(纯WORD版).files/image044.gif)
(2)设AF中点为G,连接GC,作其垂直平分线,与AF延长线交点即为圆心
由相似三角形得R′=O′G=13L/4,qvB=mv2/R′,q=/09石景山二模物理部分(纯WORD版).files/image042.gif) ,∴UNM=
,∴UNM=/09石景山二模物理部分(纯WORD版).files/image046.gif)
(3)由于粒子在磁场中运动周期T=/09石景山二模物理部分(纯WORD版).files/image048.gif) ,T与速率无关粒子撞击BC中点和DE中点后回到G,用时最短圆周半径R″=3L/2,得到最短时间t=
,T与速率无关粒子撞击BC中点和DE中点后回到G,用时最短圆周半径R″=3L/2,得到最短时间t=/09石景山二模物理部分(纯WORD版).files/image050.gif) =
=/09石景山二模物理部分(纯WORD版).files/image052.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com