
题目列表(包括答案和解析)
定义在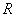 上的函数
上的函数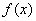 满足数列
满足数列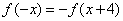 ,当
,当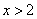 时,
时,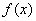 单调递增。如果
单调递增。如果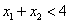 ,且
,且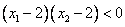 ,则
,则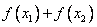 的值 ( )
的值 ( )
A.恒小于0 B.恒大于0 C.可能为0 D.可正可负
已知a, b是异面直线,下面四个命题:
①过a至少有一个平面平行于b; ②过a至少有一个平面垂直于b;
③至多有一条直线与a,b都垂直;④至少有一个平面与a,b都平行。[来源:ZXXK]
其中正确命题的个数是
A.0 B.1 C.2 D.3
| A.0 | B.1 | C.2 | D.3 |
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
D
D
A
A
C
C
A
D
B
D
二、填空题:(本题每小题4分,共16分)
13。-1 14、-2 15、{x|-2<x<-1或0<x<1或2<x<3} 16、
三、解答题:(本题共76分)
17.(1)∵这辆汽车在第一、二个交通岗均未遇到红灯,而第三个交通岗遇到红灯

(2) ∽
∽

18.解(1)令 则2bx2+x+a=0
则2bx2+x+a=0
由题意知:x=1,2是上方程两根,由韦达定理:
 ∴
∴
(2)由(1)知:
令 解得:x<0或1<x<2
解得:x<0或1<x<2
∴f(x)的单调增区间为(1,2) 减区间是(0,1)和(2,+ )
)
(3)由(2)知:f(x)在x1=1处取极小值,在x2=2处取极大值。
19.(1)


(2)
20、(Ⅰ)由已知
(Ⅱ)由(Ⅰ)得

21、解:(1)2- ≥0, 得
≥0, 得 ≥0, x<-1或x≥1 即A=(-∞,-1)∪[1,+
∞)
≥0, x<-1或x≥1 即A=(-∞,-1)∪[1,+
∞)
(2) 由(x-a-1)(
∵a<1,∴a+1> A, ∴
A, ∴ 或a≤-2, 而a<1,
或a≤-2, 而a<1,
∴ ≤a<1或a≤-2, 故当B
≤a<1或a≤-2, 故当B A时, 实数a的取值范围是(-∞,-2)∪[
A时, 实数a的取值范围是(-∞,-2)∪[ ,1]
,1]
22、因为 ,
,


 是“西湖函数”.
是“西湖函数”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com