质量m_A=3.0kg、长度L=0.60m、电量q=+4.0×10^-5C的导体板A在绝缘水平面上，质量m_B=1.0kg可视为质点的绝缘物块B在导体板A上的左端，开始时A、B保持相对静止一起向右滑动，当它们的速度减小到v₀=3.0m/s时，立即施加一个方向水平向左、场强大小E=1.0×10⁵N/C的匀强电场，此时A的右端到竖直绝缘挡板的距离为s，此后A、B始终处在匀强电场中，如图所示．假定A与挡板碰撞时间极短且无机械能损失，A与B之间（动摩擦因数μ₁=0.25）及A与地面之间（动摩擦因数μ₂=0.10）的最大静摩擦力均可认为等于其滑动摩擦力，g取10m/s²．试通过计算分析：（1）A在未与挡板相碰前A、B之间是否有相对滑动？（2）要使B恰好不从A上滑下，s应等于多少．

查看答案和解析>>

质量m_A=3.0kg、长度L=0.60m、电量q=4.0×10^-5C的导体板A在绝缘水平面上，质量m_B=1.0kg可视为质点的绝缘物块B在导体板A上的左端，开始时A、B保持相对静止一起向右滑动，当它们的速度减小到υ₀=3.0m/s时，立即施加一个方向水平向左、场强大小E=1.0×10⁵N/C的匀强电场，此时A的右端竖直绝缘档板的距离为S，此后A、B始终处在匀强电场中，如图所示．假定A与挡板碰撞时间极短且无机械能损失，A与B之间（动摩擦因数μ₁=0.25）及A与地面之间（动摩擦因数μ₂=0.10）最大静摩擦力均可认为等于其滑动摩擦力，g取10m/s²．试求要使B不从A上滑下，S应满足的条件．

查看答案和解析>>

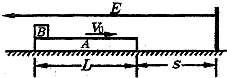
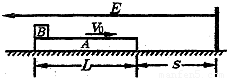质量m_A=3.0kg、长度L=0.60m、电量q=4.0×10^-5C的导体板A在绝缘水平面上，质量m_B=1.0kg可视为质点的绝缘物块B在导体板A上的左端，开始时A、B保持相对静止一起向右滑动，当它们的速度减小到υ=3.0m/s时，立即施加一个方向水平向左、场强大小E=1.0×10⁵N/C的匀强电场，此时A的右端竖直绝缘档板的距离为S，此后A、B始终处在匀强电场中，如图所示．假定A与挡板碰撞时间极短且无机械能损失，A与B之间（动摩擦因数μ₁=0.25）及A与地面之间（动摩擦因数μ₂=0.10）最大静摩擦力均可认为等于其滑动摩擦力，g取10m/s²．试求要使B不从A上滑下，S应满足的条件．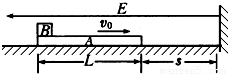

查看答案和解析>>

质量m_A=3.0kg、长度L=0.60m、电量q=+4.0×10^-5C的导体板A在绝缘水平面上，质量m_B=1.0kg可视为质点的绝缘物块B在导体板A上的左端，开始时A、B保持相对静止一起向右滑动，当它们的速度减小到v=3.0m/s时，立即施加一个方向水平向左、场强大小E=1.0×10⁵N/C的匀强电场，此时A的右端到竖直绝缘挡板的距离为s，此后A、B始终处在匀强电场中，如图所示．假定A与挡板碰撞时间极短且无机械能损失，A与B之间（动摩擦因数μ₁=0.25）及A与地面之间（动摩擦因数μ₂=0.10）的最大静摩擦力均可认为等于其滑动摩擦力，g取10m/s²．试通过计算分析：（1）A在未与挡板相碰前A、B之间是否有相对滑动？（2）要使B恰好不从A上滑下，s应等于多少．

查看答案和解析>>

质量m_A=3.0kg、长度L=0.60m、电量q=+4.0×10^-5C的导体板A在绝缘水平面上，质量m_B=1.0kg可视为质点的绝缘物块B在导体板A上的左端，开始时A、B保持相对静止一起向右滑动，当它们的速度减小到v₀=3.0m/s时，立即施加一个方向水平向左、场强大小E=1.0×10⁵N/C的匀强电场，此时A的右端到竖直绝缘挡板的距离为s，此后A、B始终处在匀强电场中，如图所示．假定A与挡板碰撞时间极短且无机械能损失，A与B之间（动摩擦因数μ₁=0.25）及A与地面之间（动摩擦因数μ₂=0.10）的最大静摩擦力均可认为等于其滑动摩擦力，g取10m/s²．试通过计算分析：（1）A在未与挡板相碰前A、B之间是否有相对滑动？（2）要使B恰好不从A上滑下，s应等于多少．

查看答案和解析>>

题号

考    点

要求

答    案

分值

1

电磁波谱

Ⅰ

D

48分

2

热学

Ⅰ

A

3

波

Ⅰ

ABC

4

圆周运动  万有引力

Ⅱ

D

5

磁场

Ⅰ

A

6

光学

Ⅱ

AB

7

力学

Ⅱ

B

8

电学

Ⅱ

BD

9.(1)

实验

Ⅰ

1.000

5分

(2)

实验

Ⅱ

  I₁、I₂分别为电流表A1A2的示数

12分

10

圆周运动  万有引力

Ⅰ

I≥

16分

11

电磁感应综合

Ⅱ

V_m＝

18分

12

力、能、动量观点综合应用

Ⅱ

2≤S

21分

附注：

10．解：I≥（设星球表面附近的重力加速度为g，由竖直上抛运动公式t=。当小球恰好能做完整的圆周运动时，设最高点的速度为v’，由mg=m有v’＝，此时经过最高点细绳刚好松弛，小球对细绳无力作用，则小球在最低点的最大速度为v_max。则由机械能守恒定律和动量定理有即 I≥。

11．解：V_m＝(线框必然同时有两条边切割磁感线而产生感应电动势。线框切割磁感线的速度为v=v₀-v_m①，（当线框以最大速度v_m匀速行驶时）线框产生的感应电动势为E＝2BLv ②，线框中产生的感应电流为I＝ ③，线框所受安培力为F_安=2BIL ④，线框匀速行驶时，据平衡条件可得F_安=F ⑤，解得V_m＝。)

12．解：设B受到的最大静摩擦力为f_1m，则f_1m=μ₁m_Bg=2.5N  ①，设A受到的滑动摩擦力为f₂，则f₂=μ₂(m_A+m_B)g=4.0N ②，施加电场后，设A、B以相同的加速度向右做匀减速运动，加速度大小为a，由牛顿第二定律qE+f₂=(m_A+m_B)a ③，解得a=2.0m/s²。设B受到的摩擦力为f₁，由牛顿第二定律得f_­1=m_Ba ④，解得f₁=2.0N，由于f₁<f­_1m，所以电场作用后，A、B仍保持相对静止以相同加速度a向右做匀减速运动，A与挡板碰前瞬间，设A、B向右的共同速度为v₁，v₁²=v₀²－2aS ⑤，A与挡板碰后，以A、B系统为研究对象 qE=f₂ ⑥，故A、B系统动量守恒，设A、B向左共同速度为v，规定向左为正方向m_Av₁－m_Bv₁=(m­_A+m_B)v ⑦，设该过程中，B相对于A向右的位移为S₁，A向左的位移为S₂，由系统功能关系qES₂－μ₁mgS₁－μ₂(m_A+m_B)gS₂＝(m_A+m_B)v²－(m_A+m_B)v₁² ⑧，[或写为μ₁m_BgS­₁＝(m_A+m_B)v₁²－(m_A+m_B)v²，同样给这4分]，A、B达到共同速度v后做匀速运动，要使B不从A上滑下S₁≤L ⑨，解⑤⑦⑧⑨代入数据得S≥2.0m。