练习册

  • 练习册
  • 试题
    (2)细绳被拉断时.cd棒的速度.(3)细绳刚被拉断时.cd棒下落的速度. 【查看更多】

     

    题目列表(包括答案和解析)

    （12分）如图所示，两根水平放置的平行光滑导轨上，有两根可以移动的、垂直导轨的导体棒和，导轨的间距为25cm，棒和棒的阻值均为2，导轨的电阻不计。现将棒用一根绝缘细绳水平拉住，细绳所能承受的最大拉力为2N。整个装置处于竖直向上的匀强磁场中，磁感应强度为4T。今在棒上作用一个与导轨平行向右的恒力，直到细绳被拉断。则细绳被拉断时，求：

     

    （1）cd棒中电流强度的大小；

    （2）ab棒的速度大小。

    查看答案和解析>>

    （12分）如图所示，两根水平放置的平行光滑导轨上，有两根可以移动的、垂直导轨的导体棒和，导轨的间距为25cm，棒和棒的阻值均为2，导轨的电阻不计。现将棒用一根绝缘细绳水平拉住，细绳所能承受的最大拉力为2N。整个装置处于竖直向上的匀强磁场中，磁感应强度为4T。今在棒上作用一个与导轨平行向右的恒力，直到细绳被拉断。则细绳被拉断时，求：

     

    （1）cd棒中电流强度的大小；

    （2）ab棒的速度大小。

    查看答案和解析>>

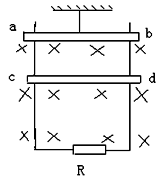    如图所示，足够长的两根光滑导轨相距0.5m竖直平行放置，导轨电阻不计，下端连接阻值为1Ω的电阻R，导轨处在匀强磁场B中，磁场的方向垂直于导轨平面向里，磁感应强度为0.8T。两根质量均为0.04kg、电阻均为0.5Ω的水平金属棒ab、cd都与导轨接触良好，金属棒ab用一根细绳悬挂，细绳允许承受的最大拉力为0.64N，现让cd棒从静止开始落下，直至细绳刚好被拉断，在此过程中电阻R上产生的热量为0.2J，g=10/s2。求：

    （1）此过程中ab棒和cd棒分别产生的热量Qab和Qcd。

    （2）细绳被拉断时，cd棒的速度。

    （3）细绳刚被拉断时，cd棒下落的高度。

    查看答案和解析>>

    如图所示，足够长的两根光滑导轨相距0.5m竖直平行放置，导轨电阻不计，下端连接阻值为1Ω的电阻R，导轨处在匀强磁场B中，磁场的方向垂直于导轨平面向里，磁感应强度为0.8T。两根质量均为0.04kg、电阻均为0.5Ω的水平金属棒ab、cd都与导轨接触良好，金属棒ab用一根细绳悬挂，细绳允许承受的最大拉力为0.64N。现让cd棒从静止开始落下，直至细绳刚好被拉断，在此过程中电阻R上产生的热量为0.2J，g取10m／s2，求：
    （1）此过程中ab棒和cd棒分别产生的热量Qab和Qcd；
    （2）细绳刚被拉断时，cd棒的速度；
    （3）细绳刚被拉断时，cd棒下落的高度；
    （4）cd棒从静止开始落下直至细绳刚好被拉断所经过的时间。

    查看答案和解析>>

    如图所示，相距0.5m足够长的两根光滑导轨与水平面成37°角，导轨电阻不计，下端连接阻值为2Ω的电阻R，导轨处在磁感应强度B=2T的匀强磁场中，磁场方向垂直导轨平面斜向上。ab、cd为水平金属棒且与导轨接触良好，它们的质量均为0.5kg、电阻均为2Ω。ab棒与一绝缘水平细绳相连处于静止状态，现让cd棒从静止开始下滑，直至与ab相连的细绳刚好被拉断，在此过程中电阻R上产生的热量为0.5J，已知细线能承受的最大拉力为5N．求细绳被拉断时：（g=10m/s2，sin37°=0.6）

    （1）ab棒中的电流大小；

    （2）cd棒的速度大小；

    （3）cd棒下滑的距离。

    查看答案和解析>>

    14.A  15.C  16.B  17.AD  18.B  19.CD  20.D   21.ACD 

    22解．（17分）（1）2.094～2.098mm 

    （2）①C  E  ②C中未记下两条细绳的方向  E中未说明是否把橡皮条的结点拉到了位置O  （3）①B    D   ②见图

    评分标准：（1）3分  （2）中①问每空2分；②问每空1分。共6分。（3）中①问每空2分；②问4分，电流表外接正确或变阻器分压连接正确均可各得1分，完全正确的得4分；若变阻器限流连接正确，其它连接无误，可给2分。共8分。

    23．（16分）解答：（1）跳起后重心升高 

    h=2.25－2.10=0.15m        （1分）

    根据机械能守恒定律         ①        （4分）

    解得      ②                （2分）

    （2）由动量定理（F－mg）t=mv－0              ③            （4分）

    即  ④                          （2分）

    将数据代入上式可得F=(100       +700)N⑤          （2分）

    根据牛顿第三定律可知：上跳过程中他对地面的平均压力F′=(100       +700)N(1分）

    24、解答：（19分）（1）设电场强度为E，把小球A、B看作一个系统，由于绳未断前作匀速运动，则有

    2qE=3mg，E=3mg/2q                    (3分）

    绳断后，根据牛顿第二定律：

    对A：qE-mg=maA      

    得aA=g/2，方向坚直直向上  （3分）

    对B：qE-2mg=2maB

    得aB=-g/4，负号表示方向坚直直向下　　（3分）

    （2）细绳断开前后两球组成系统合外力为零，满足总动量守恒，设B球速度为零时，A球的速度为vA,

    根据动量守恒定律得：

     (m+2m）v0=mvA­+0  　　　　　 （3分）

    vA=3 v0                                                (1分)

    (3)由运动学公式:vt2-v02=2as

    得sA=(3 v0)2- v02/２aA=(3 v0)2- v02/g=8 v02/g　　　　(3分)

    由功能关系，电场力对Ａ做的功等于物体Ａ的机械能增量：

    △ＥA=qEsA=12m v02　　　　　　　　　　　　　(3分)

    25．解：（1）金属棒cd从静止开始运动直至细绳刚好被拉断的过程中有：

    Qab =U2t/Rab      ①   (2分)

    QR=U2t/R         ②  (1分)

    联立①②可得Qab=0.4J    ③  (1分)

    Qcd =I2Rcdt          ④   (2分)

    Qab + QR =I2RRabt/(Rab+R) ⑤(1分)

    联立④⑤可得Qab =0.9J ⑥  (1分)

    (2) 细绳被拉断瞬时,对ab棒有:

    Fm=mg+BIabL        ⑦   (2分)

    又有IR=RabIab/R      ⑧   ( 1分)

    Icd=Iab+Icd            ⑨      (1分)

    又由闭合欧姆定可得

    BLv=Icd [Rcd+RabR/(Rab+R)]  ⑩   (2分)

    联立⑦⑧⑨⑩可得v=1.88m/s ?   (1分)

    (3)由功能关系得

    Mgh= Q总 +1/2mv2         ?(4分))

    即可得h=3.93m           ? ((1分))

     

     

     

     


    同步练习册答案