
题目列表(包括答案和解析)
设函数 ,
, ,则
,则 的值域是( )
的值域是( )
A. B.
B. C.
C. D.
D.
第II卷(非选择题,共90分)
已知![]() 均为正数,
均为正数,![]() ,则
,则![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,将答案填在题中的横线上。
正项数列![]() 的前n项的乘积
的前n项的乘积![]() ,则数列
,则数列![]() 的前n项和
的前n项和![]() 中的最大值是 ( )
中的最大值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
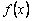 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在 上为增函数,
上为增函数,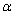 、
、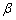 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )
A. B.
B.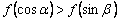
C.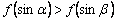 D.
D.
第Ⅱ卷(非选择题,共90分)
若函数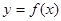 在区间[a,b]上的图象为连续不断的一条曲线,则下列说法正确的是( )
在区间[a,b]上的图象为连续不断的一条曲线,则下列说法正确的是( )
A.若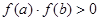 ,不存在实数
,不存在实数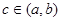 使得
使得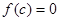 ;
;
B.若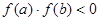 ,存在且只存在一个实数
,存在且只存在一个实数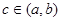 使得
使得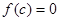 ;
;
C.若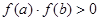 ,有可能存在实数
,有可能存在实数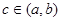 使得
使得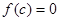 ;
;
D.若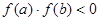 ,有可能不存在实数
,有可能不存在实数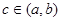 使得
使得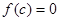
第Ⅱ卷(非选择题 共90分)
一.选择题
序号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
B
D
D
C
A
A
C
B
D
A
二填空题
13. 2或8; 14. ;
15.
;
15. ; 16.
; 16. .
.
三.解答题
17.解:(Ⅰ)
 ………………………………………………………………4分
………………………………………………………………4分
 …………………………6分
…………………………6分
(Ⅱ) …………………………………………………8分
…………………………………………………8分

∴ …………………………………………………………………………10分
…………………………………………………………………………10分
 ………………………………………………………………………………12分
………………………………………………………………………………12分
18.解:(Ⅰ)在Rt△ABC中,AB=1,∠BAC=60°,∴BC= ,AC=2.
,AC=2.
在Rt△ACD中,AC=2,∠CAD=60°,∴CD=2 ,AD=4.
……………………………2分
,AD=4.
……………………………2分
∴ =
=
 .………………………………………………………………4分
.………………………………………………………………4分
则V= . ……………………………………………………………… 6分
. ……………………………………………………………… 6分
(Ⅱ)∵PA=CA,F为PC的中点,∴AF⊥PC. ……………………………………8分
∵PA⊥平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC.∴CD⊥PC.
∵E为PD中点,F为PC中点,∴EF∥CD.则EF⊥PC. ………………………………10分
∵AF∩EF=F,∴PC⊥平面AEF.………………………………………………………………12分
19.设第一个匣子里的三把钥匙为A,B,C,第二个匣子里的三把钥匙为a,b,c(设A,a能打开所有门,B只能打开第一道门,b只能打开第二道门,C,c不能打开任何一道门)
(Ⅰ)第一道门打不开的概率为 ;……………………………………………………………5分
;……………………………………………………………5分
(Ⅱ)能进入第二道门的情况有Aa,Ab,Ac,Ba,Bb,而二把钥匙的不同情况有Aa,Ab,Ac,Ba,Bb,Bc,Ca,Cb,Cc共9种,故能进入第二道门的概率为 ……………………………………………………………12分
……………………………………………………………12分
20.(Ⅰ)依题



即
 (
( …………………………………………………3分
…………………………………………………3分
故 为等差数列,a1=1,d=2
为等差数列,a1=1,d=2
 ………………………………………………………………………………………………5分
………………………………………………………………………………………………5分
(Ⅱ)设公比为q,则由b1b2b3=8,bn>0 …………………………………………………6分
…………………………………………………6分
又 成等差数列
成等差数列
 ………………………………………………………………………………………8分
………………………………………………………………………………………8分
 或
或 …………………………………………………………………………………10分
…………………………………………………………………………………10分
 或
或 ……………………………………………………………………12分
……………………………………………………………………12分
21解:(Ⅰ)依题PN为AM的中垂线

 …………………………………………………2分
…………………………………………………2分
又C(-1,0),A(1,0)
所以N的轨迹E为椭圆,C、A为其焦点…………………………………………………………4分
a= ,c=1,所以
,c=1,所以 为所求………………………………………………………5分
为所求………………………………………………………5分
(Ⅱ)设直线 的方程为:y=k(x-1),代入椭圆E的方程:x2+2y2=2得:
的方程为:y=k(x-1),代入椭圆E的方程:x2+2y2=2得:
(1+2k2)x2-4k2x+2k2-2=0………………(1)
设G(x1,y1)、H(x2,y2),则x1,x2是(1)的两个根.
 …………………………………………………………7分
…………………………………………………………7分
依题


 ………………………………………………………9分
………………………………………………………9分
解得: ………………………………………………………………………12分
………………………………………………………………………12分
22.解法(一):
 时,
时, 即
即 ……①
……①
⑴ 时,
时, 恒成立,
恒成立,
⑵ 时,①式化为
时,①式化为 ……②
……②
⑶ 时,①式化为
时,①式化为 ……③…………………………………………………5分
……③…………………………………………………5分
记 ,则
,则 …………………………7分
…………………………7分



所以

故由② ,由③
,由③ ………………………………………………………………………13分
………………………………………………………………………13分
综上 时,
时, 在
在 恒成立.………………………………………………14分
恒成立.………………………………………………14分
解法(二):
 时,
时, 即
即 ……①
……①
⑴ 时,
时, ,
, ,不合题意…………………………………………………2分
,不合题意…………………………………………………2分
⑵ 恒成立
恒成立
∴ 在
在 上为减函数,
上为减函数,
得 ,矛盾,…………………………………………………………………………………5分
,矛盾,…………………………………………………………………………………5分
⑶ ,
, =
=

若 则
则 ,
, ,故在[-1,1]内,
,故在[-1,1]内,
 ,得
,得 ,矛盾.
,矛盾.
若

依题意, 解得
解得 即
即
综上 为所求.……………………………………………………………………………14分
为所求.……………………………………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com