
题目列表(包括答案和解析)
 如图所示,轻弹簧的左端固定,右端与质量为m的物块B相连,B静止在粗糙水平面上的O点,此时弹簧处于原长.另一质量与B相同的物块A从P点以速度v0开始向B滑行,当A滑过距离l时,与B发生正碰,碰撞时间极短,碰后A、B粘在一起向左运动,A、B压缩弹簧后恰好能够返回并停在O点. 设A和B均可视为质点,它们与水平面的动摩擦因数均为μ.重力加速度为g.求:
如图所示,轻弹簧的左端固定,右端与质量为m的物块B相连,B静止在粗糙水平面上的O点,此时弹簧处于原长.另一质量与B相同的物块A从P点以速度v0开始向B滑行,当A滑过距离l时,与B发生正碰,碰撞时间极短,碰后A、B粘在一起向左运动,A、B压缩弹簧后恰好能够返回并停在O点. 设A和B均可视为质点,它们与水平面的动摩擦因数均为μ.重力加速度为g.求: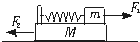 如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间接触光滑.开始时,m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个运动过程中,弹簧形变不超过其弹性限度,对于m、M和弹簧组成的系统( )
如图所示,一轻弹簧左端固定在长木板M的左端,右端与小木块m连接,且m、M及M与地面间接触光滑.开始时,m和M均静止,现同时对m、M施加等大反向的水平恒力F1和F2,从两物体开始运动以后的整个运动过程中,弹簧形变不超过其弹性限度,对于m、M和弹簧组成的系统( )如图所示,与轻弹簧相连的物体A停放在光滑的水平面上,物体B沿水平方向向右运动,跟与A相连的轻弹簧相碰.在B跟弹簧相碰后,下列说法中正确的是
A.当弹簧压缩最大时,木块B减少的动能最多
B.从B跟弹簧相碰到弹簧压缩最大的过程中,系统的总动能不断减小
C.从B跟弹簧相碰到弹簧压缩最大的过程中,系统的总动量不断减小
D.物体A的速度最大时,弹簧的弹性势能为零
如图甲所示,一轻弹簧的两端与质量分别为m1和m2的两物块A、B的连接,并静止在光滑的水平面上,现使A瞬时获得水平向右的速度v0,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示。求:
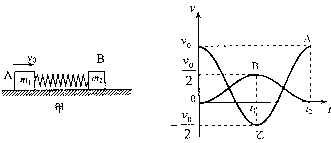
(1)两物块质量之比m1:m2多大?
(2)当A物体的速度最小时,弹簧的弹性势能![]() 多大?(计算结果用m1和v0表示)
多大?(计算结果用m1和v0表示)
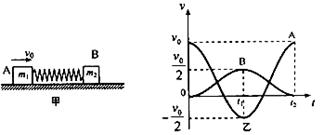
如图甲所示,一轻弹簧的两端与质量分别为m1和m2的两物块A、B的连接,并静止在光滑的水平面上,现使A瞬时获得水平向右的速度v0,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示。求:
(1)两物块质量之比m1:m2多大?
(2)当A物体的速度最小时,弹簧的弹性势能![]() 多大?(计算结果用m1和v0表示)
多大?(计算结果用m1和v0表示)
一、选择题:(每题3分共45分)(本题共15小题;每小题分,共45分。在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确。全部选对的得3分,选对.不全的得2分,有选错或不答的得0分。)
1
2
3
4
5
6
7
8
D
CD
B
A
ABC
A
D
C
9
10
11
12
13
14
15
D
C
BD
ABD
BD
ABD
AB
二、实验填空题(本大题共二题九空;每空2分,共18分。)
16 2mm 5.50m 3.30 5.45m
17.(1) 64.7(2) ABD (3)A、B、
18. 碰撞依据动量守衡有: mv0=(M+m)v v=5m/s
由平抛规律得下落时间为0.5秒
平抛初速度为4米/秒
由动能定理解得摩擦因数为0.3
19.解:(1)对m据动量定理有I0=mv0
当二者速度相同时(设为v),弹性势能最大,对系统由动量守恒定律得mv0=(M+m)v
联立可解得:v=1m/s
(2)最终二者有相同速度(即为u),由动量守恒和功能关系得
mv0=(m+M)u


联立可解得:Emax = 3J Lmax = 0.75m
20.解:对子弹和木块应用动量守恒定律:

所以 
对子弹、木块由水平轨道到最高点应用机械能守恒定律,取水平面为零势能面:有

所以 
由平抛运动规律有: ……①
……①
 …… ②
…… ②
解①、②两式有 
所以,当R = 0.2m时水平距离最大
最大值Smax = 0.8m。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com