如右图中A和B表示在真空中相距为d的两平行金属板加上电压后，它们之间的电场可视为匀强电场；右边表示一周期性的交变电压的波形，横坐标代表时间t，纵坐标代表电压U_AB，从t=0开始，电压为给定值U₀，经过半个周期，突然变为-U₀……。如此周期地交替变化。在t=0时刻将上述交变电压U_AB加在A、B两极上，电子质量为m，电量为e，求：

1.在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最大，则所加交变电压的频率最大不能超过多少?

2.在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最小(零)，则所加交变电压的频率为多大?

3.在t=?时刻释放上述电子，在一个周期时间，该电子刚好回到出发点?

试说明理由并讨论物理量间应满足什么条件。

如右图中A和B表示在真空中相距为d的两平行金属板加上电压后，它们之间的电场可视为匀强电场；右边表示一周期性的交变电压的波形，横坐标代表时间t，纵坐标代表电压U_AB，从t=0开始，电压为给定值U₀，经过半个周期，突然变为-U₀……。如此周期地交替变化。在t=0时刻将上述交变电压U_AB加在A、B两极上，电子质量为m，电量为e，求：

1.在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最大，则所加交变电压的频率最大不能超过多少?

2.在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最小(零)，则所加交变电压的频率为多大?

3.在t=?时刻释放上述电子，在一个周期时间，该电子刚好回到出发点?

试说明理由并讨论物理量间应满足什么条件。

.如右图中A和B表示在真空中相距为d的两平行金属板加上电压后，它们之间的电场可视为匀强电场；右边表示一周期性的交变电压的波形，横坐标代表时间t，纵坐标代表电压U_AB，从t=0开始，电压为给定值U₀，经过半个周期，突然变为-U₀……。如此周期地交替变化。在t=0时刻将上述交变电压U_AB加在A、B两极上，电子质量为m，电量为e，求：

(1)在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最大，则所加交变电压的频率最大不能超过多少?

(2)在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最小(零)，则所加交变电压的频率为多大?

(3)在t=?时刻释放上述电子，在一个周期时间，该电子刚好回到出发点?

试说明理由并讨论物理量间应满足什么条件。

右图中A和B表示在真空中相距为d的两平行金属板加上电压后，它们之间的电场可视为匀强电场；右边表示一周期性的交变电压的波形，横坐标代表时间t，纵坐标代表电压U_AB，从t=0开始，电压为给定值U₀，经过半个周期，突然变为-U₀……。如此周期地交替变化。在t=0时刻将上述交变电压U_AB加在A、B两极上，求：

(1)?在t=0时刻，在B的小孔处无初速地释放一电子，在t=3T/4时电子的速度大小？（一个周期内电子不会打到板上，T作为已知）

(2) 在t=?时刻释放上述电子，在一个周期时间，该电子刚好回到出发点?试说明理由并具备什么条件。?

(3)在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最小(零)，则所加交变电压的周期为多大?

（4）在t=0时刻，在B的小孔处无初速地释放一电子，要想使这电子到达A板时的速度最大，则所加交变电压的周期最小为多少?

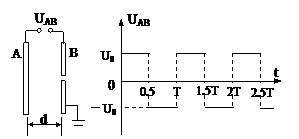
[来源:Z*xx*k.Com]