
题目列表(包括答案和解析)
光滑水平面上放着质量,mA=1kg的物块A与质量mB=2kg的物块B, A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B 不动,此时弹簧弹性势能EP=49J。在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示。放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5m, B恰能到达最高点C。取g=10m/s2,求
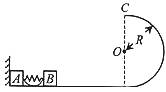 (1)绳拉断后瞬间B的速度vB的大小;
(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I 的大小;
(3)绳拉断过程绳对A所做的功W。
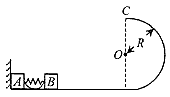
光滑水平面上放着质量,mA=1kg的物块A与质量mB=2kg的物块B, A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能EP=49J。在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示。放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5m, B恰能到达最高点C。g=10m/s2,求
(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I 的大小;
(3)绳拉断过程绳对A所做的功W。
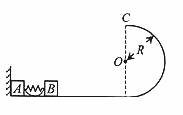
光滑水平面上放着质量mA=1kg的物块A与质量mB=2kg的物块B, A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B 不动,此时弹簧弹性势能EP=49J。在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示。放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5m, B恰能到达最高点C。g=10m/s2,求

(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I 的大小;
(3)绳拉断过程绳对A所做的功W。
光滑水平面上放着质量mA=1kg的物块A与质量mB=2kg的物块B, A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B 不动,此时弹簧弹性势能EP=49J。在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示。放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5m, B恰能到达最高点C。g=10m/s2,求
(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I的大小;
(3)绳拉断过程绳对A所做的功W。
1、B C 2、C 3、A 4、A 5、B 6、B C 7、CD 8、B 9、A 10、C 11、 BD
12、 A 13、C 14、AB 15、C D
16、C
17、[⑴当最靠近上表面的烟尘颗粒被吸附到下板时,烟尘就被全部吸附。烟尘颗粒受到的电场力F=qU/L,L=at2/2=qUt2/2mL,故t=0.02s
⑵W=NALqU/2=2.5×10-4J
⑶设烟尘颗粒下落距离为x,则当时所有烟尘颗粒的总动能
EK=NA(L-x) mv2/2= NA(L-x) qUx/L,当x=L/2时EK达最大,而x=at12/2,故t1=0.014s ]
18..files/image047.gif)
19. .files/image049.gif)
20. 解:由图象可知,.files/image051.gif) =
=
(1)当波向右传播时,点B的起振方向竖直向下,包括P点在内的各质点的起振方向均为竖直向下.
①波速.files/image053.gif) ,由
,由.files/image055.gif) ,得
,得.files/image057.gif) .
.
②由t= 0至P点第一次到达波峰止,经历的时间.files/image059.gif) ,而t=0时O点的振动方向竖直向上(沿y轴正方向),故经
,而t=0时O点的振动方向竖直向上(沿y轴正方向),故经.files/image061.gif) 时间,O点振动到波谷,即
时间,O点振动到波谷,即.files/image063.gif)
(2)当波速v=.files/image065.gif) ,即
,即.files/image067.gif) ,实线波形变为虚线波形经历了
,实线波形变为虚线波形经历了.files/image069.gif) ,故波沿x轴负方向传播.
,故波沿x轴负方向传播.
21解:(1)对整体由动量守恒定律得
.files/image071.gif) ,则
,则.files/image073.gif) ,方向向右.
,方向向右.
(2)由功能关系得.files/image075.gif) ,则
,则.files/image077.gif)
(3)①物体A、B未相碰撞,B停止时,A继续运动,此时小
车开始运动.对小车应用动能定理得.files/image079.gif) ,则
,则.files/image081.gif)
②物体B速度为零时正好与A相撞,碰后小车开始加速,最终达到共同速度.files/image083.gif) .对小车应用动能定理得
.对小车应用动能定理得.files/image085.gif) ,则
,则.files/image087.gif)
.files/image089.jpg) 所以小车位移大小的取值范围是
所以小车位移大小的取值范围是.files/image091.gif)
.files/image093.gif)
22、【解析】电子在两极板间运动的V-t图象如右图所示。
(1)要求电子到达A板的速度最大,则电子应该从B板一直加速运动到A板,即电子从B板加速运动到A板所用时间必须满足:
t≤.files/image095.gif) ①
①
依题意知:S=.files/image097.gif) ×
×.files/image099.gif) ×t2=d ②
×t2=d ②
综合①、②可得:f≤.files/image101.gif) 。
。
(2)由电子在电场中运动时的受力情况及速度变化情况可知:要求电子到达A板的速度为零,则电子应该在t=nT(n=1,2,3,…)时刻到达A板,电子在每个.files/image103.gif) 内通过的位移为:
内通过的位移为:
S=.files/image097.gif) ×
×.files/image099.gif) ×(
×(.files/image103.gif) )2
③
)2
③
依题意知:d=n(2S) ④
综合③、④可得:f=.files/image106.gif) (n=1,2,3,…)。
(n=1,2,3,…)。
(3)在t=T/4时刻释放电子,经过一个周期,在t=.files/image108.gif) 时刻,电子刚回到出发点。条件是在半个周期即从(
时刻,电子刚回到出发点。条件是在半个周期即从(.files/image110.gif) ~
~.files/image112.gif) )时间内,电子的位移小于d,亦即频率f≥
)时间内,电子的位移小于d,亦即频率f≥.files/image114.gif) 。
。
【本题小结】解答带电粒子在交变电场中加速运动的问题,可借助于带电粒子在交变电场中运动的速度图象加以分析。
23.(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com