
题目列表(包括答案和解析)
| 4π2n2L |
| t2 |
| 4π2n2L |
| t2 |
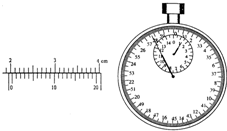 在做“用单摆测定重力加速度”的实验中,某同学先测得摆线长为92.50cm,然后用秒表记录了单摆做45次全振动的时间,摆球的直径和秒表的读数如图所示,该单摆的摆长为
在做“用单摆测定重力加速度”的实验中,某同学先测得摆线长为92.50cm,然后用秒表记录了单摆做45次全振动的时间,摆球的直径和秒表的读数如图所示,该单摆的摆长为4π2n2(L0+
| ||
| t2 |
4π2n2(L0+
| ||
| t2 |
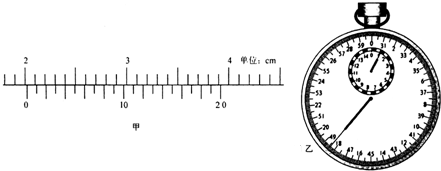
 在做“用单摆测定重力加速度”的实验中,
在做“用单摆测定重力加速度”的实验中,4π2n2(L0+
| ||
| t2 |
4π2n2(L0+
| ||
| t2 |
| 4π2 |
| k |
| 4π2 |
| k |
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
D
AB
AC
D
CD
AB
B
D
二、实验题:
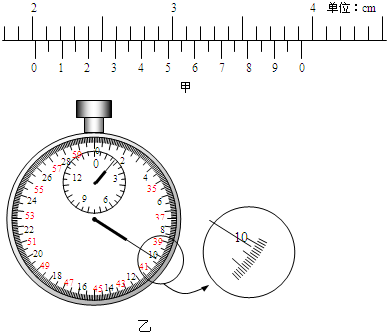
11、0.874;1.88;9.75
12、(1)  ;
; ; 0 ;
; 0 ;
 ;
;
(2)①让球A多次从同一位置摆下,求B球落点的平均位置;②
 角取值不要太小;
角取值不要太小;
③两球A、B质量不要太小;④球A质量要尽量比球B质量大
三、计算题:
13、f=6000N,P=120000w
14、(1)对平板车施加恒力F后,平板车向右做匀减速直线运动,车向左的加速度大小为
a= m/s2
m/s2
小球到达左端A时,车向右的位移 s= =
=
此时车向右的速度 v1= =
=
小球到达左端A所用时间设为t1,则 =0.5s
=0.5s
小球离开车后做自由落体运动,设下落时间为t2 ,则 h=
|