
题目列表(包括答案和解析)
求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面。
在平面直角坐标系中,已知三个点列![]() ,其中
,其中![]() ,满足向量
,满足向量![]() 与向量
与向量![]() 平行,并且点列
平行,并且点列![]() 在斜率为6的同一直线上,
在斜率为6的同一直线上,![]() 。
。
证明:数列![]() 是等差数列;
是等差数列;
试用![]() 与
与![]() 表示
表示![]() ;
;
设![]() ,是否存在这样的实数
,是否存在这样的实数![]() ,使得在
,使得在![]() 与
与![]() 两项中至少有一项是数列
两项中至少有一项是数列![]() 的最小项?若存在,请求出实数
的最小项?若存在,请求出实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
若![]() ,对于区间[0,1]上的任意l,总存在不小于2的自然数k,当n??k时,
,对于区间[0,1]上的任意l,总存在不小于2的自然数k,当n??k时,![]() 恒成立,求k的最小值.
恒成立,求k的最小值.
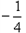 ,设动点M的轨迹为曲线C,
,设动点M的轨迹为曲线C,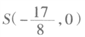 ,证明:
,证明: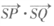 为定值。
为定值。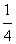 x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.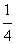 p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)=
p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)=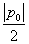 ;
;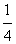 p12),E′(p2,
p12),E′(p2,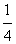 p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X
p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X |P1|>|P2|
|P1|>|P2| φ(a,b)=
φ(a,b)=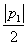 ;
;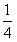 (x+1)2-
(x+1)2-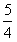 },当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。
},当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。在复平面内,  是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。
(Ⅰ)如果点A关于实轴的对称点为点B,求向量 对应的复数
对应的复数 和
和 ;
;
(Ⅱ)复数 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
【解析】第一问中利用复数的概念可知得到由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i ∵
=-2i ∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
=
第二问中,由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
(Ⅰ)由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i 3分
=-2i 3分
∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
= 2分
2分
(Ⅱ)A、B、C、D四点在同一个圆上。 2分
证明:由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
一、选择题(每题5分共50分)
1.D 2.A 3.B 4.C 5.C
6.C 7.B 8.C 9.C 10.D
二、填空题(每题5分共20分)
11..files/image176.gif) 12.
12..files/image178.gif) 13.
13..files/image180.gif)
14.(0,2),.files/image182.gif) 15.3
15.3
三、解答题(共80分)
16.解:(Ⅰ)由已知得:.files/image184.gif) ,
,
又.files/image186.gif) 是△ABC的内角,所以
是△ABC的内角,所以.files/image188.gif) .
.
(2)由正弦定理:.files/image190.gif) ,
,.files/image192.gif)
又因为.files/image194.gif) ,
,.files/image196.gif) ,又
,又.files/image198.gif) 是△ABC的内角,所以
是△ABC的内角,所以.files/image200.gif) .
.
17.证明:连结AB,A1D,在正方形中,A1B=A1D,O是BD中点,
∴A1O⊥BD;
连结OM,A.files/image202.gif) a=MC1
a=MC1
OA=OC=.files/image204.gif) a,AC=
a,AC=.files/image206.gif) a,
a,
∴A1O2=A.files/image202.gif) a2=
a2=.files/image209.gif) a2,OM2=OC2+MC2=
a2,OM2=OC2+MC2=.files/image211.gif) a2,A
a2,A.files/image213.gif) a2=
a2=.files/image215.gif) a2,∴A
a2,∴A
∴A1O⊥OM,
∴AO1⊥平面MBD
18解:(Ⅰ).files/image217.gif) ,
,
因为函数.files/image168.gif) 在
在.files/image220.gif) 及
及.files/image222.gif) 取得极值,则有
取得极值,则有.files/image224.gif) ,
,.files/image226.gif) .
.
即.files/image228.gif)
解得.files/image230.gif) ,
,.files/image232.gif) .
.
(Ⅱ)由(Ⅰ)可知,.files/image234.gif) ,
,
.files/image236.gif) .
.
当.files/image238.gif) 时,
时,.files/image240.gif) ;
;
当.files/image242.gif) 时,
时,.files/image244.gif) ;
;
当.files/image246.gif) 时,
时,.files/image240.gif) .
.
所以,当.files/image220.gif) 时,
时,.files/image168.gif) 取得极大值
取得极大值.files/image251.gif) ,又
,又.files/image253.gif) ,
,.files/image255.gif) .
.
则当.files/image257.gif) 时,
时,.files/image168.gif) 的最大值为
的最大值为.files/image255.gif) .
.
因为对于任意的.files/image257.gif) ,有
,有.files/image262.gif) 恒成立,
恒成立,
所以 .files/image264.gif) ,
,
解得 .files/image266.gif) 或
或.files/image268.gif) ,
,
因此.files/image270.gif) 的取值范围为
的取值范围为.files/image272.gif) .
.
19.解(Ⅰ)由题意知.files/image274.gif) ,
,.files/image276.gif)
.files/image278.gif)
当n≥2时,.files/image280.gif) ,
,.files/image282.gif) ,
,
两式相减得 .files/image284.gif)
整理得:.files/image286.gif)
∴数列{.files/image288.gif) }是以2为首项,2为公比的等比数列。
}是以2为首项,2为公比的等比数列。
∴.files/image290.gif)
(Ⅱ)由(Ⅰ)知.files/image292.gif) ,∴bn=n
,∴bn=n.files/image294.gif)
.files/image296.gif) , …………①
, …………①
.files/image298.gif) , …………②
, …………②
①-②得
.files/image300.gif) ,
,
∴.files/image302.gif) ,
,
∴.files/image304.gif) ,
,
20.解:设这台机器最佳使用年限是n年,则n年的保养、维修、更换易损零件的总费用为:
.files/image306.gif)
.files/image308.gif) ,
,
.files/image310.gif)
.files/image312.gif)
等号当且仅当.files/image314.gif)
.files/image316.gif)
答:这台机器最佳使用年限是12年,年平均费用的最小值为1.55万元.
21.⑴c=2, a=3 双曲线的方程为
⑵ 得 (1?3k2)x2?6kx?9=0
x1+x2= , x1x2=
由△>0 得 k2<1
由= x1x2+y1y2=(1+k2) x1x2+k(x1+x2)+2>2得 <k2<3
所以,<k2<1
即k∈(?1, )∪( , 1 )
附加题
(1)证明:先将.files/image168.gif) 变形:
变形:.files/image319.gif) ,
,
当.files/image166.gif) ,即
,即.files/image322.gif) 时,∴
时,∴.files/image324.gif) 恒成立,
恒成立,
故.files/image168.gif) 的定义域为
的定义域为.files/image326.gif) 。
。
反之,若.files/image168.gif) 对所有实数
对所有实数.files/image038.gif) 都有意义,则只须
都有意义,则只须.files/image329.gif) 。
。
令.files/image331.gif) ,即
,即.files/image333.gif) ,解得
,解得.files/image322.gif) ,故
,故.files/image166.gif) 。
。
(2)解析:设.files/image335.gif) ,
,
∵.files/image337.gif) 是增函数,
是增函数,
∴当.files/image339.gif) 最小时,
最小时,.files/image168.gif) 最小。
最小。
而.files/image341.gif) ,
,
显然,当.files/image343.gif) 时,
时,.files/image339.gif) 取最小值为
取最小值为.files/image345.gif) ,
,
此时.files/image347.gif) 为最小值。
为最小值。
(3)证明:当.files/image166.gif) 时,
时,.files/image349.gif) ,
,
当且仅当m=2时等号成立。
∴.files/image351.gif) 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com