如图所示，A为位于一定高度处的质量为m=1×10^-5 kg带电荷量为q=+1×10^-6 C的微粒，B为位于水平地面上的质量为M的用特殊材料制成的长方形空心盒子，盒子与地面间的动摩擦因数为μ=0.2，盒内存在着竖直向上的匀强电场，场强大小E=1×10³ N/C，盒外存在着竖直向下的匀强电场，场强大小也为E=1×10³ N/C，盒的上表面开有一系列略大于微粒的小孔，孔间距满足一定的关系，使得微粒进出盒子的过程中始终不与盒子接触。当微粒A以1 m/s的速度从孔1进入盒子的瞬间，盒子B恰以v₁=0.4 m/s的速度向右滑行。设盒子足够长，取重力加速度g为10m/s²，不计微粒的重力，微粒恰能顺次从各个小孔进出盒子。试求：
（1）从微粒第一次进入盒子至盒子停止运动的过程中，盒子通过的总路程；
（2）微粒A从第一次进入盒子到第二次进入盒子所经历的时问；
（3）盒子上至少要开多少个小孔，才能保证微粒始终不与盒子接触。

查看答案和解析>>

如图所示，质量m=50kg的运动员（可视为质点），在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳，轻绳另一端系在距离水面高H=10.0m的O点，此时轻绳与竖直方向的夹角为θ=37°，C点是位于O点正下方水面上的一点，距离C点x=4.8m处的D点有一只救生圈，O、A、C、D各点均在同一竖直面内．若运动员抓紧绳端点，从台阶上A点沿垂直于轻绳斜向下以一定初速度v₀跃出，当摆到O点正下方的B点时松开手，最终恰能落在救生圈内．（sin37°=0.6，cos37°=0.8，g=10m/s²）求：
（1）运动员经过B点时速度的大小v_B；
（2）运动员从台阶上A点跃出时的动能E_k；
（3）若初速度v₀不一定，且使运动员最终仍能落在救生圈内，则救生圈离C点距离x将随运动员离开A点时初速度v₀的变化而变化．试在下面坐标系中粗略作出x-v₀的图象，并标出图线与x轴的交点．

查看答案和解析>>

如图所示，物体在蒙有动物毛皮的斜面上运动．由于毛皮表面的特殊性，引起物体的运动有如下特点：①顺着毛的生长方向运动时毛皮产生的阻力可以忽略；②逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力，且动摩擦因数μ恒定．斜面顶端距水平面高度为h=0.8m，质量为m=2kg的小物体M从斜面顶端A由静止滑下，从O点进入光滑水平滑道时无机械能损失，为使M制动，将轻弹簧的一端固定在水平滑道延长线B处的墙上，另一端恰位于水平轨道的中点C．已知斜面的倾角θ=53⁰，动摩擦因数均为μ=0.5，其余各处的摩擦不计，g=10m/s²，下滑时逆着毛的生长方向，求：
（1）弹簧压缩到最短时的弹性势能（设弹簧处于原长时弹性势能为零）
（2）若物块M能够被弹回到斜面上，则它能够上升的最大高度是多少？
（3）物块M在斜面上下滑过程中的总路程

查看答案和解析>>

如图所示，水平地面M点左侧粗糙，右侧光滑．整个空间有一场强大小E₁=1×10³N/C、方向竖直向下的匀强电场．质量m_A=0.04kg的不带电小物块A用长为R=5m不可伸长的绝缘轻质细绳拴于O点，静止时与地面刚好接触．带正电的小物块B与左端固定在墙上的绝缘轻弹簧接触但不粘连，B的质量m_B=0.02kg，带电量为q=+2×10^-4 C，与M左侧地面间动摩擦因数μ=0.5．现用水平向左的推力将B由M点（弹簧原长处）缓慢推至P点（弹簧仍在弹性限度内），推力做功W=2.65J，MP之间的距离为L=50cm．撤去推力，B向右运动，随后与A发生正碰并瞬间成为一个整体C（A、B、C均可视为质点）．已知碰撞前后电荷量保持不变，碰后C的速度为碰前B速度的

1

3

．碰后立即把匀强电场方向变为竖直向上，场强大小变为E₂=6×10³N/C．（取g=10m/s²）求：
（1）B与A碰撞过程中损失的机械能．
（2）碰后C是否立即做圆周运动？如果是，求C运动到最高点时绳的拉力大小；如果不是，则C运动到什么位置时绳子再次绷紧？

查看答案和解析>>

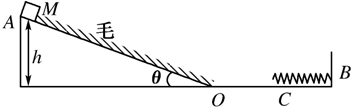
如图所示，某货场需将质量为m₁=100kg的货物（可视为质点）从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物由轨道顶端无初速滑下，轨道半径R=1.8m．地面上紧靠轨道依次排放两块完全相同的木板A、B，长度均为l=2m，质量均为m₂=100kg，木板上表面与轨道末端相切．货物与木板间的动摩擦因数为μ₁，木板与地面间的动摩擦因数μ₂=0.2．（最大静摩擦力与滑动摩擦力大小相等，取g=10m/s²）
（1）求货物到达圆轨道末端时对轨道的压力．
（2）若货物滑上木板A时，木板不动，而滑上木板B时，木板B开始滑动，求μ₁应满足的条件．
（3）若μ₁=0.5，求货物滑到木板A末端时的速度和在木板A上运动的时间．
（4）求货物停止的位置到A板右端的距离？

查看答案和解析>>

1．(3-4模块) (1)CD  (2)y的负方向(1分)、0.4(1分)、1.9(1分)

(3)解：a.由折射定律：  

在BC界面：sin60°=sinγ  ①（1分）          γ=30⁰°                          

∵sinC=     ②（1分）

∴光线在AC界面发生反射再经AB界面折射 （1分）

sin30°=sinγ^/             ③（1分）

γ^/=60°  则射出光线与AB面的夹角　　β=90°-γ^/=30°  ④（1分）            

2．（1）v₂=0.390m/s(2分) ，a=0.600 m/s²(2分)(说明：取两位有效数字共扣1分)

（2），----1分   ------1分--------1分

若F反比于△t^-2，则加速度正比于外力。

15．（1）30.5-30.9 mＡ；1.5×10³ Ω。×10 ，欧姆调零。

（2）①如图；         (2分)

     ②(A^-1)                (2分)

     ③ 0.10-0.14Ω (2分)、9.00-9.60Ω/m(2分)

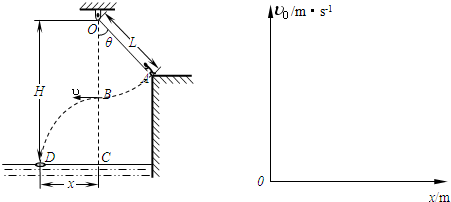
3、（16分）（1）（5分）设物块块由D点以初速做平抛，落到P点时其竖直速度为

                 得

       平抛用时为t，水平位移为s，

       在桌面上过B点后初速

       BD间位移为     则BP水平间距为

   （2）（5分）若物块能沿轨道到达M点，其速度为

       轨道对物块的压力为F_N，则

解得   即物块不能到达M点

   （3）（6分）设弹簧长为AC时的弹性势能为E_P，物块与桌面间的动摩擦因数为，

       释放      释放

       且

       在桌面上运动过程中克服摩擦力做功为W_f，

       则   可得

4．17. （共14分）解：（1）微粒在盒子内、外运动时，盒子的加速度a^’=μMg/M＝μg＝0.2×10 m/s²=2 m/s²

盒子全过程做匀减速直线运动，所以通过的总路程是：（4分）

（2）A在盒子内运动时，   方向以向上为正方向

由以上得　　a＝qE/m=1×10^-6×1×10³/1×10^-5 m/s²=1×10² m/s² （2分）

A在盒子外运动时，   则a＝qE/m=1×10² m/s²  方向向下

A在盒子内运动的时间t₁＝2v/ a＝2×1/1×10²s＝2×10^-2s

同理A在盒子外运动的时间t₂＝2×10^-2s

A从第一次进入盒子到第二次进入盒子的时间t= t₁＋t₂＝4×10^-2s    （4分）

（3）微粒运动一个周期盒子减少的速度为△v= a^’ （t₁＋ t₂）=2×（0.02＋0.02）=0.08m/s

从小球第一次进入盒子到盒子停下，微粒球运动的周期数为n=v₁/△v=0.4/0.08=5

故要保证小球始终不与盒子相碰，盒子上的小孔数至少为2n+1个，即11个． （4分）

5. ⑴1N，向右（提示：注意相当于左右两个边都以v₀=10m/s向左切割磁感线，产生的感应电动势相加，左右两边都受到安培力作用，且方向都向右。）⑵8m/s（提示：车运动起来后，当车对地的速度为v时，线框切割磁感线的相对速度变为(v₀- v)，当安培力与阻力平衡时达到最大速度。）；⑶100m（提示：先求出最大共同速度为5m/s，撤去磁场后对A和P整体用动能定理。）

6.解：（1）子弹打击滑块，满足动量守恒定律，设子弹射入滑块后滑块的速度为v₁，则

          ①     （4分）

（2）从O到A滑块做加速度增大的减速运动，从A到O滑块可能做加速度增大的减速运动，或先做加速度减小的加速运动再做加速度增大的减速运动。

滑块向右到达最右端时，弹簧的弹性势能最大。设在OA段克服摩擦力做的功为W_f，与滑块的动摩擦因数为μ，弹性势能最大值为E_p，根据能量守恒定律：

    ②                       （2分）

由于滑块恰能返回到O点，返回过程中，根据能量守恒定律：

（3）设第二颗子弹射入滑块后滑块的速度为v₂，由动量守恒定律得：

     （2分）

如果滑块第一次返回O点时停下，则滑块的运动情况同前，对该过程应用能量守恒定律：

        ⑥

①②③④⑤⑥联立解得

如果滑块第三次返回O点时停下，对该过程由能量守恒：

①②③④⑥⑦联立解得

所以，滑块仅两次经过O点，第二颗子弹入射速度的大小范围在