
题目列表(包括答案和解析)
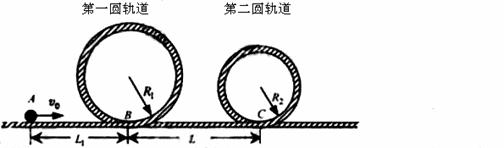
(14分)下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的二个圆形轨道组成,B、C分别是二个圆形轨道的最低点, BC 间距L=12.5m,第一圆形轨道半径R1=1.4m。一个质量为![]() kg的小球(视为质点),从轨道的左侧A点以
kg的小球(视为质点),从轨道的左侧A点以![]() 的初速度沿轨道向右运动。小球与水平轨道间的动摩擦因数
的初速度沿轨道向右运动。小球与水平轨道间的动摩擦因数![]() ,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。计算结果保留小数点后一位数字。试求
,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。计算结果保留小数点后一位数字。试求
(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离。
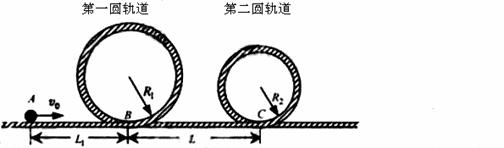
下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的二个圆形轨道组成,B、C分别是二个圆形轨道的最低点, BC 间距L=12.5m,第一圆形轨道半径R1=1.4m。一个质量为![]() kg的小球(视为质点),从轨道的左侧A点以
kg的小球(视为质点),从轨道的左侧A点以![]() 的初速度沿轨道向右运动。小球与水平轨道间的动摩擦因数
的初速度沿轨道向右运动。小球与水平轨道间的动摩擦因数![]() ,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。计算结果保留小数点后一位数字。试求
,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。计算结果保留小数点后一位数字。试求
(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离。
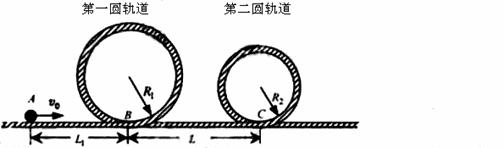
下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的二个圆形轨道组成,B、C分别是二个圆形轨道的最低点, BC 间距L=12.5m,第一圆形轨道半径R1=1.4m。一个质量为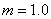 kg的小球(视为质点),从轨道的左侧A点以
kg的小球(视为质点),从轨道的左侧A点以 的初速度沿轨道向右运动。小球与水平轨道间的动摩擦因数
的初速度沿轨道向右运动。小球与水平轨道间的动摩擦因数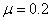 ,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。计算结果保留小数点后一位数字。试求
,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。计算结果保留小数点后一位数字。试求
(1)如果小球恰能通过第一圆形轨道,AB间距L1应是多少;
(2)在满足(1)的条件下,如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围;
(3)小球最终停留点与起点A的距离。
如下图(a)所示,小车放在斜面上,车前端拴有不可伸长的细线,跨过固定在斜面边缘的小滑轮与重物相连,小车后面与打点计时器的纸带相连.起初小车停在靠近打点计时器的位置,重物到地面的距离小于小车到滑轮的距离.启动打点计时器,释放重物,小车在重物的牵引下,由静止开始沿斜面向上运动,重物落地后,小车会继续向上运动一段距离.打点计时器使用的交流电频率为50 Hz.下图(b)中a、b、c是小车运动纸带上的三段,纸带运动方向如箭头所示.

(1)根据所提供纸带上的数据,计算打c段纸带时小车的加速度大小为________m/s2.(结果保留两位有效数字)
(2)打a段纸带时,小车的加速度是2.5 m/s2.请根据加速度的情况,判断小车运
动的最大速度可能出现在b段纸带中的________.
(3)如果取重力加速度为10 m/s2,由纸带数据可推算出重物与小车的质量比为________.
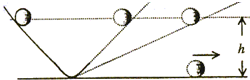 如图所示,伽利略理想实验将可靠的事实和理论思维结合起来,能更深刻地反映自然规律.伽利略的斜面实验程序如下:
如图所示,伽利略理想实验将可靠的事实和理论思维结合起来,能更深刻地反映自然规律.伽利略的斜面实验程序如下:一、选择题:
1. C 2.B 3.D 4.B 5.A 6.C 7.A 8.C 9.C 10.A
11. D 12.B 13.B 14.C 15.BC 16.A 17.BD 18.ABC 19.D 20.BCD
21.D
二、非选择题:t
22.(1)每空2分 计6分
相邻相等时间间隔内的位移差(或△s)相等 匀加速直线运动3.5
(2)①连线正确得4分,电路设计错误得0分,设计正确,连线错误得2分
②U,I,L,d(3分) ③h= (3分)
(3分)
23.O→B
(1)h= .t3=
.t3= …………5分
…………5分
(2)B→A v0=gt g=
g= =3.56(m/s2) …………5分
=3.56(m/s2) …………5分
(3)O→B F-mg=ma ① …………2分
vB=at1 ② …………2分
F=m( )=1.5×103(
)=1.5×103( )=1.63×104(N) …………3分
)=1.63×104(N) …………3分
24.(1)在D点处
F=Bqv1 ① …………2分
FN-mg-F=0 ② …………2分
A→D:mv0=Mv2+mv1 ③ …………3分
△E= ④ …………3分
④ …………3分
解①②③④得△E=18J …………2分
(2)m再次回到D点时M有最大速度
mv1+Mv2=mv3+Mv4 ⑤ …………3分
 ⑥ …………2分
⑥ …………2分
解①②③④⑤⑥可得 v4=3(m/s) …………2分
25.(1) x ① …………2分
x ① …………2分
Ek= ② …………2分
② …………2分
解①②得 Ek= …………2分
…………2分
(2)Uc=ε= =kπr2 ③ …………2分
=kπr2 ③ …………2分
当k有极小值时: ④ …………2分
④ …………2分
解③④得:Kmin= …………2分
…………2分
当k有极大值时: ⑤ …………2分
⑤ …………2分
 ⑥ …………2分
⑥ …………2分
解③⑤⑥得:Kmax= …………2分
…………2分
∴ …………2分
…………2分
26.H+、Cl-,Na+、OH-,NH4Cl,NH4Cl,NH4Cl、NH3?H2O,NH4Cl、HCl
27.(1)MnO2>Cl2>H2O2>H2SO4(或X>C>B>D)
(2)H∶ ∶
∶
(3)Cu+2H2SO4(浓) CuSO4+2H2O+SO2↑ H2O2+Cl2=2HCl+O2
CuSO4+2H2O+SO2↑ H2O2+Cl2=2HCl+O2
(4)SO2+2H2O+Cl2=4H++SO 2Cl-
2Cl-
(5)A、B(3分)
28.(1)b c e a
(2)①反应放热,使溶液温度升高,反应速率增大,
②产生的气体将酸液压到‘U’型管右边,使酸液与Cu丝脱离
(3)‘U’型管左端产生无色气体形成一段气柱,无色气体变为红棕色
(4)①2NO+O2=2NO2,3NO2+H2O=2HNO3+NO
或4NO+3O2+2H2O=4HNO3(4分) ②mol/L ③19
29.(1)C (2)BC (3)酯化、消失、聚合(或缩聚)



 CHCOOH CHO
CHCOOH CHO

 (4)
(4)
OH CHOHCH2OH

 CHO COONH4
CHO COONH4


 (5)
+2Ag(NH3)2OH
(5)
+2Ag(NH3)2OH +2Ag↓+
+2Ag↓+
 CHOHCH2OH CHOHCH2OH
CHOHCH2OH CHOHCH2OH
3NH3+H2O …………3分
注:26~29题中未注明分值的空格,每空2分
30.(21分)
(1)将从S型活细菌中提取出的DNA、蛋白质和多糖等物质,分别加入已培养了R型细菌的培养基中,培养并观察菌落的情况。(4分)
(2)①已灭活的病原微生物体内的抗原物质仍能引起机体的免疫反应(4分)
②体液免疫(2分)
(3)①注射外源抗体可使机体获得一定的免疫能力(3分)
②第二步:选取数只相似的小白鼠,分成数量相等的A、B两组,A组先注射免疫血清,再注射破伤风外毒素,B组内注射破伤风外毒素。(6分)
③A组小鼠正常生活,B组小鼠死亡(2分)
31.(21分)
CH2―CH2―COOH
 |
 (1)H2N―C―COOH (2分); GAG(2分)
(1)H2N―C―COOH (2分); GAG(2分)
H
(2)异养需氧型(2分) 溶氧不足(或通气量不足)(2分)
(3)步骤:菌种的选取、培养基的配制、灭菌、扩大培养(4分)时期:稳定期(2分)
特点:菌体的出生率等于死亡率,且活菌数目达到最大,细胞内大量积累代谢产物,特别是次级代谢产物(4分)
(4)原因:①保证微生物对营养物质的需求;②排出部分有害代谢产物;③使微生物保持较长时间的快速生长.(答一点即可)(3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com