
题目列表(包括答案和解析)
如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.(1)求证:EF是⊙O的切线;(2)若AE=3,BF=2,求⊙O的半径.
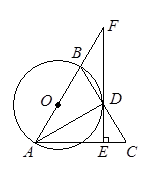
【解析】(1)连接OD,利用切线性质求证
(2)设⊙O的半径为x.通过△ODF∽△AEF,解得x的值
如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.(1)求证:EF是⊙O的切线;(2)若AE=3,BF=2,求⊙O的半径.
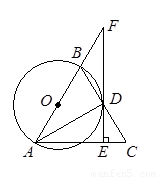
【解析】(1)连接OD,利用切线性质求证
(2)设⊙O的半径为x.通过△ODF∽△AEF,解得x的值
在△ABC中,AB=AC,∠ACB =∠ABC,CG⊥BA交BA的延长线于点G,一等腰三角板按如图27-1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边

在一条直线上,另一条直角边恰好经过点B。
(1)在图24-1中请你通过观察,测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后说明你的猜想。
(2)当三角尺沿AC方向平移到图24-2所在的位置时,一条直角边仍与AC边在同一直线上,另
一条直角边交BC边于点D,过点D作DE⊥BA于点E,此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后说明你的猜想。
(提示:过点D作DH⊥CG,可得四边形EDHG是长方形,而且∠HDC=∠ABC,ED=GH)
(3)当三角尺在(2)的基础上沿AC方向继续平移到图24-3所示的位置(点F在线段AC上,
且点F与点C不重合)时,试猜想DE、DF与CG之间满足的数量关系?(不用说明理由)
【解析】本题利用等腰直角三角形的性质及全等三角形的判定和性质求解
在△ABC中,AB=AC,∠ACB =∠ABC,CG⊥BA交BA的延长线于点G,一等腰三角板按如图27-1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边

在一条直线上,另一条直角边恰好经过点B。
(1)在图24-1中请你通过观察,测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后说明你的猜想。
(2)当三角尺沿AC方向平移到图24-2所在的位置时,一条直角边仍与AC边在同一直线上,另
一条直角边交BC边于点D,过点D作DE⊥BA于点E,此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后说明你的猜想。
(提示:过点D作DH⊥CG,可得四边形EDHG是长方形,而且∠HDC=∠ABC,ED=GH)
(3)当三角尺在(2)的基础上沿AC方向继续平移到图24-3所示的位置(点F在线段AC上,
且点F与点C不重合)时,试猜想DE、DF与CG之间满足的数量关系?(不用说明理由)
【解析】本题利用等腰直角三角形的性质及全等三角形的判定和性质求解
课外兴趣小组活动时,老师提出了如下问题:
如图,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连结BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.

感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)问题解决:
受到(1)的启发,请你证明下面命题:如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连结EF.

①求证:BE+CF>EF
②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.
(3)问题拓展:
如图,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连结EF,探索线段BE、CF、EF之间的数量关系,并加以证明.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com