练习册

  • 练习册
  • 试题
    ∴.∴MC=15k. 【查看更多】

     

    题目列表(包括答案和解析)

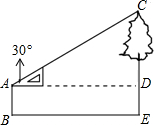    如图，一学生要测量校园内一颗水杉树的高度，他站在距离水杉树10m的B处，测得树顶的仰角为∠CAD=30°，已知测角仪的架高AB=2m，那么这棵水杉树高是（　　）

    查看答案和解析>>

    如图所示，在正三角形ABC内有一点M，且MA=3，MB=4，MC=5．
    （1）求∠BMA的度数；
    （2）求正三角形ABC的面积．
    （提示：把△ACM绕点A逆时针旋转60°，使点C与点B重合）

    查看答案和解析>>

    下列运算中，正确的是（　　）
    A、
    6a+1
    3
    =2a+1
    B、3mn-3n=m
    C、x2+x2=x4
    D、3a+2a=5a

    查看答案和解析>>

    精英家教网已知：如图，把矩形OCBA放置于直角坐标系中，OC=3，BC=2，取AB的中点M，连接MC，把△MBC沿x轴的负方向平移OC的长度后得到△DAO．
    （1）试直接写出点D的坐标；
    （ 2 ）已知点B与点D在经过原点的抛物线上，点P在第一象限内的该抛物线上移动，过点P作PQ⊥x轴于点Q，连接OP．若以O、P、Q为顶点的三角形与△DAO相似，试求出点P的坐标；
    （3）试问在（2）抛物线的对称轴上是否存在一点T，使得
    |TO-TB|的值最大？若存在，则求出点T点的坐标；若不存在，则说明理由．

    查看答案和解析>>

    已知：直线AB：y=
    12
    x+3与x轴交于点A，与y轴交于点B，另外有点C（0，2）和点M（m，0）．⊙M以MC为半径，⊙M与直线AB相切，求经过点A、B、M的抛物线的解析式．

    查看答案和解析>>


    同步练习册答案