
题目列表(包括答案和解析)
(本题14分).在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, .以
.以 的中点
的中点 为球心、
为球心、 为直径的球面交
为直径的球面交 于点
于点 ,交
,交 于点
于点 .
.
(1)求直线 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(2)求点 到平面
到平面 的距离.
的距离.
(本题14分).在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, .以
.以 的中点
的中点 为球心、
为球心、 为直径的球面交
为直径的球面交 于点
于点 ,交
,交 于点
于点 .
.
(1)求直线 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(2)求点 到平面
到平面 的距离.
的距离.
(本题14分).在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() .以
.以![]() 的中点
的中点![]() 为球心、
为球心、![]() 为直径的球面交
为直径的球面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
 (1)求直线
(1)求直线![]() 与平面
与平面![]() 所成的角的正弦值;
所成的角的正弦值;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
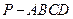 中,底面
中,底面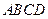 是矩形,
是矩形,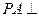 平面
平面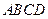 ,
,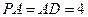 ,
,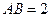 .以
.以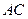 的中点
的中点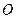 为球心、
为球心、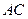 为直径的球面交
为直径的球面交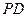 于点
于点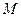 ,交
,交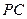 于点
于点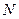 .
.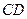 与平面
与平面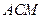 所成的角的正弦值;
所成的角的正弦值;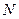 到平面
到平面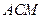 的距离.
的距离.| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽y(颗) | 23 | 25 | 30 | 26 | 16 |
| ? |
| y |
| |||||||
|
. |
| y |
. |
| x |
| ? |
| y |
| ? |
| y |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com