
题目列表(包括答案和解析)
已知数列![]() 的通项公式
的通项公式![]() 和前
和前![]() 项和
项和![]() ,
,![]() 是
是![]() 与2的等差中项,数列
与2的等差中项,数列![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上。
上。
(1)求数列![]() 与
与![]() 的通项
的通项![]() ,
,![]() ;
;
(2)设![]() 的前
的前![]() 项和为
项和为![]() ,比较
,比较![]() 与2的大小;
与2的大小;
(3)设![]() 若
若![]() (
(![]() ),求C的最小值
),求C的最小值
数列![]() 的前
的前![]() 项和为
项和为![]() ;数列
;数列![]() 中,
中,![]() ,且对任意
,且对任意![]() ,
,
(1)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(2)设 ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() 。
。
数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;
;
(1)求![]() 与
与![]() 的关系式,并求
的关系式,并求![]() 的通项公式;
的通项公式;
(2)求和![]() ;
;
数列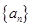 的前
的前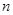 项和为
项和为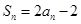 ,数列
,数列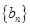 是首项为
是首项为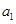 ,公差不为零的等差数列,且
,公差不为零的等差数列,且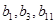 成等比数列.
成等比数列.
(1)求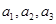 的值;
的值;
(2)求数列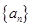 与
与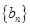 的通项公式;
的通项公式;
(3)求证: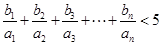
已知数列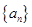 的首项
的首项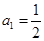 ,前
,前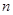 项和
项和 .(Ⅰ)求数列
.(Ⅰ)求数列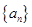 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设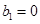 ,
, ,
,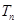 为数列
为数列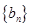 的前
的前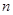 项和,求证:
项和,求证: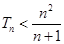 .
.
【解析】本试题主要是考查了数列的前n项和与通项公式之间关系的运用。以及数列的前n项和的运用。
一、选择题:
1.解析:B.由 且
且 能够推出
能够推出 ;反之,由
;反之,由 只能推出
只能推出 或
或 ,而不能推出
,而不能推出 且
且 .故“
.故“ ”是“
”是“ 且
且 ”的必要不充分条件,故选B.
”的必要不充分条件,故选B.
评析:有关充要条件的判定问题,概念性较强,进行判断时,必须紧扣概念.一方面,要正确理解充要条件本身的概念,进行双向推理,准确判断;另一方面,还要注意根据具体问题所涉及到的数学概念来思考.本题中,弄清并集和交集概念中“或”与“且”的关系显得很重要.
|