
题目列表(包括答案和解析)
 如图,正三棱锥
如图,正三棱锥 ,
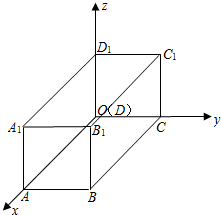
,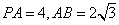 ,D为BC的中点, E为AP的中点.P在底面△ABC内的射影为O,以O为坐标原点,OD、OP所在直线分别为Y、Z轴建立如图所示的空间直角坐标系O—XYZ.
,D为BC的中点, E为AP的中点.P在底面△ABC内的射影为O,以O为坐标原点,OD、OP所在直线分别为Y、Z轴建立如图所示的空间直角坐标系O—XYZ.
⑴ 写出点A、B、D、E的坐标;
⑵ 用向量法求异面直线AD与BE所成的角.
 如图,以长方体ABCD-A1B1C1D1的一个顶点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.已知点B1的坐标是(2,1,1).
如图,以长方体ABCD-A1B1C1D1的一个顶点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系.已知点B1的坐标是(2,1,1).| AD1 |
| A1C1 |
| BA1 |
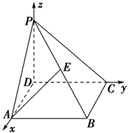 如图所示,PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<
如图所示,PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<| DP |
| AE |
| ||
| 3 |
 在矩形ABCD中,|AB|=2
在矩形ABCD中,|AB|=2| 3 |
| |OR| |
| |OF| |
| |CR′| |
| |CF| |
| 1 |
| n |
| x2 |
| 3 |
| 2 |
| 3 |
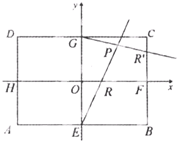 (2013•黄冈模拟)在矩形ABCD中,|AB|=2
(2013•黄冈模拟)在矩形ABCD中,|AB|=2| 3 |
| |OR| |
| |OF| |
| |CR′| |
| |OF| |
| 1 |
| n |
| x2 |
| 3 |
| 2 |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com