（08年唐山市二模）设，则函数的定义域为

     A．（1，2）      B．      C．      D．

设椭圆的左、右顶点分别为，点在椭圆上且异于两点，为坐标原点.

（Ⅰ）若直线与的斜率之积为，求椭圆的离心率；

（Ⅱ）若，证明直线的斜率 满足

【解析】(1)解：设点P的坐标为.由题意，有  ①

由，得，

由，可得，代入①并整理得

由于，故.于是，所以椭圆的离心率

（2）证明：（方法一）

依题意，直线OP的方程为，设点P的坐标为.

由条件得消去并整理得  ②

由，及，

得.

整理得.而，于是，代入②，

整理得

由，故，因此.

所以.

(方法二)

依题意，直线OP的方程为，设点P的坐标为.

由P在椭圆上，有

因为，，所以，即   ③

由，，得整理得.

于是，代入③，

整理得

解得，

所以.

（本小题满分12分）已知二次函数满足：，，且该函数的最小值为2.

⑴ 求此二次函数的解析式;

⑵ 若函数的定义域为= .(其中). 问是否存在这样的两个实数,使得函数的值域也为?若存在,求出的值;若不存在,请说明理由.

函数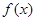的定义域为D，若存在闭区间[a，b]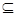D，使得函数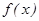满足：

(1) 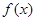在[a，b]内是单调函数；(2) 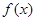在[a，b]上的值域为[2a，2b]，则称区间[a，b]为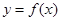的“和谐区间”．下列函数中存在“和谐区间”的是            (只需填符合题意的函数序号)

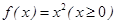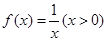①； ②； ③； ④．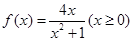

（08年潮州市二模理）（14分）已知函数的导数满足，常数为方程的实数根．

⑴ 若函数的定义域为I，对任意，存在，使等式=成立，

 求证：方程不存在异于的实数根；

⑵ 求证：当时，总有成立；

⑶ 对任意，若满足，求证．