
题目列表(包括答案和解析)
 在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式P1P2=
在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式P1P2=| (x1-x2)2+(y1-y 2)2 |
| (-1-0)2+(2-3)2 |
| 2 |
| 13 |
| 13 |
| 13 |
| 13 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
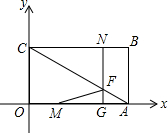
如图,在梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0),(14,3),(4,3).点P、Q同时从原点出发,分别做匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位,点Q沿OC、CB向终点B运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
 (1)设从出发起运动了x秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或CB上时的坐标(用含x的代数式表示,不要求写出x的取值范围);
(1)设从出发起运动了x秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或CB上时的坐标(用含x的代数式表示,不要求写出x的取值范围);
(2)设从出发起运动了x秒,如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半.
①试用含x的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如果有可能,求出相应的x的值和P、Q的坐标,如不可能,请说明理由.
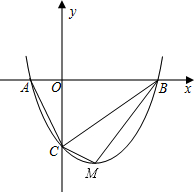 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.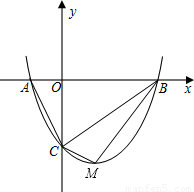
阅卷须知:
1.一律用红钢笔或红圆珠笔批阅.
2.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.
一、选择题(共8个小题,每小题4分,共32分)
题 号
1
2
3
4
5
6
7
8
答 案
B
D
A
C
B
A
D
A
二、填空题(共4个小题,每小题4分,共16分)
题 号
9
10
11
12
答 案



 (或
(或 )
)
三、解答题(共5个小题,每小题5分,共25分)
13. 解:
 …………………………………3分
…………………………………3分

 .
…………………………………5分
.
…………………………………5分
14. 解:由不等式 ,得
,得 . …………………………………1分
. …………………………………1分
由不等式 ,得
,得 .
…………………………………2分
.
…………………………………2分
∴ 原不等式组的解集是 . …………………………………3分
. …………………………………3分
在数轴上表示为:
 |
…………………………………5分
15. 解:去分母,得
 .
…………………………………2分
.
…………………………………2分
去括号,整理,得
 .
.
解得  .
…………………………………4分
.
…………………………………4分
经检验, 是原方程的根.
…………………………………5分
是原方程的根.
…………………………………5分
所以,原方程的根为 .
.
 |
16.证明:∵ 四边形ABCD是菱形,
∴  ,
, .
.
∴  . …………………2分
. …………………2分
在 和
和 中,
中,

∴  ≌
≌ .
…………………………………4分
.
…………………………………4分
∴  .
…………………………………5分
.
…………………………………5分
17.解:

 .
…………………………………3分
.
…………………………………3分
∵  ,
,
∴  .
.
即 
 .
…………………………………5分
.
…………………………………5分
四、解答题(共2个小题,每小题5分,共10分)
18. 解:(1)由题意得 ≌
≌ ,所以,
,所以, .
.
∵ 在 中,
中, ,
, ,
,
∴  .
.
∴  .即
.即 .
…………………………………1分
.
…………………………………1分
在等腰梯形 中,
中, ,
, ,∴
,∴  .
.
∴  .
…………………………………3分
.
…………………………………3分
(2)由(1)得, .
.
在 中,
中, ,
, ,
, ,
,
所以, .
…………………………………5分
.
…………………………………5分
19.(1)证明:如图,联结 .
…………………………………1分
.
…………………………………1分
 ∵
∵  ,
, ,
,
∴  .
.
∴  是等边三角形.
是等边三角形.
∴  ,
, .
.
∴  .
.
∴  .
…………………………………2分
.
…………………………………2分
所以, 是⊙
是⊙ 的切线. …………………………………3分
的切线. …………………………………3分
(2)解:作 于
于 点.
点.
∵  ,∴
,∴  .
.
又 ,
, ,所以在
,所以在 中,
中, .
.
在 中,∵
中,∵  ,∴
,∴  .
.
由勾股定理,可求 .
.
所以,
 .
…………………………………5分
.
…………………………………5分
 五、解答题(本题满分6分)
五、解答题(本题满分6分)
20. 解:
(1)10%. ……………………2分
(2)340人,见右图.……………………4分
(3)约660万人. ……………………6分
六、解答题(共2个小题,第21题4分,第22题5分,共9分)
21. 解:(1)在抛物线 中,令
中,令 ,得
,得 ,
,
解得 或
或 (
( ).所以,
).所以, ,
, .
.
∵  ,∴
,∴  .
.
所以, 点的坐标为(
点的坐标为( ,0),
…………………………………1分
,0),
…………………………………1分
 点的坐标为(
点的坐标为( ,
, ).
…………………………………2分
).
…………………………………2分
(2) 的面积
的面积
 ,所以,当
,所以,当 时,
时, .
.
…………………………………4分
 22. 解:(1)跳棋子跳过路径及各点字母如图.
22. 解:(1)跳棋子跳过路径及各点字母如图.
………………3分
(2)跳跃15次后,停在 处,
处,
过 作
作
 ,垂足为
,垂足为 点,
点,
则
 ;
;
由 ,∴
,∴ 
 .
.
…………………………………5分
七、解答题(本题满分7分)
23.(1)证明:设 ,
, ,
, ,
, 与
与 的面积分别为
的面积分别为 ,
, ,矩形
,矩形 的面积为
的面积为 .
.
由题意,得  ,
, ,
, .
.
∴  ,
, ,
, .
.
∴  .
.
∴ 四边形 的面积是定值.
…………………………………2分
的面积是定值.
…………………………………2分
 (2)解:由(1)可知
(2)解:由(1)可知 ,则
,则 .
.
又∵  ,
,
∴  .
.
∵  ,
, ,
,
∴  .
.
∴  . …………………………………4分
. …………………………………4分
(3)解:①由题意知: . …………………………………5分
. …………………………………5分
② 、
、 两点坐标分别为
两点坐标分别为 ,
, ,
,
∴  .
.
∴  .
.
∴  .
.
∴ 当 时,
时, 有最大值
有最大值 .
…………………………………7分
.
…………………………………7分
八、解答题(本题满分7分)
24.解:(1)如图(1),当 时,
时, 的
的 边与⊙
边与⊙ 相切;
相切;
如图(2),当 时,
时, 的
的 边与⊙
边与⊙ 相切;
相切;
如图(3),当 时,
时, 的
的 边与⊙
边与⊙ 相切;
相切;
如图(4),当 时,
时, 的
的 边所在直线与⊙
边所在直线与⊙ 相切.
相切.
…………………………………4分
(2)由(1),可知,当 和
和 时,半圆
时,半圆 与直线
与直线 围成的区域与
围成的区域与
三边围成的区域有重叠部分,如图(2)、(3)的阴影部分所示,重叠部分的面积分别为 和
和 .
.
…………………………………7分
 |
 |
 |
|||
 |
九、解答题(本题满分8分)
25.(1)证明:∵  ,∴
,∴  .∴
.∴  .
.
又∵  ,∴
,∴  .
.
∴  .∴
.∴  ∽
∽ . …………………………………2分
. …………………………………2分
 (2)证明:如图,过点
(2)证明:如图,过点 作
作
 ,交
,交 于点
于点 ,
,
∵  是
是 的中点,容易证明
的中点,容易证明 .
.
在 中,∵
中,∵  ,∴
,∴  .
.
∴ 
 .
.
∴  .
…………………………………5分
.
…………………………………5分
(3)解: 的周长
的周长
 ,
, .
.
设 ,则
,则 .
.
∵  ,∴
,∴  .即
.即 .
.
∴  .
.
由(1)知 ∽
∽ ,
,
∴ 


 .
.
∴  的周长
的周长
 的周长
的周长 .
.
∴  的周长与
的周长与 值无关.
…………………………………8分
值无关.
…………………………………8分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com