
题目列表(包括答案和解析)
数列![]() 的前
的前![]() 项和记作
项和记作![]() ,满足
,满足![]() ,
,![]() .
.
![]() 求出数列
求出数列![]() 的通项公式.
的通项公式.
(2)![]() ,且
,且![]() 对正整数
对正整数![]() 恒成立,求
恒成立,求![]() 的范围;
的范围;
(3)(原创)若![]() 中存在一些项成等差数列,则称
中存在一些项成等差数列,则称![]() 有等差子数列,若
有等差子数列,若![]() 证明:
证明:![]() 中不可能有等差子数列(已知
中不可能有等差子数列(已知![]() 。
。
数列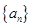 的前
的前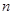 项和记为
项和记为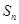 ,
, ,
,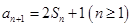 .
.
(1)求数列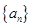 的通项公式;
的通项公式;
(2)等差数列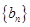 的前
的前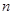 项和
项和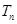 有最大值,且
有最大值,且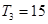 ,又
,又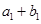 、
、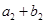 、
、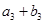 成等比数列,求
成等比数列,求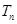 .
.
数列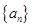 的前
的前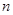 项和记为
项和记为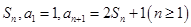
(Ⅰ)求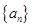 的通项公式;
的通项公式;
(Ⅱ)等差数列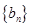 的各项为正,其前
的各项为正,其前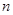 项和为
项和为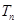 ,且
,且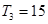 ,又
,又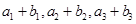 成等比数列,求
成等比数列,求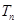
数列 的前
的前 项和记为
项和记为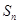 ,
, ,
, .
.
(I)当 为何值时,数列
为何值时,数列 是等比数列?
是等比数列?
(II)在(I)的条件下,若等差数列 的前
的前 项和
项和 有最大值,且
有最大值,且 ,又
,又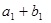 ,
, ,
, 成等比数列,求
成等比数列,求 .
.
数列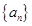 的前
的前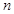 项和记为
项和记为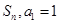 ,
,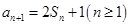
(Ⅰ)求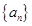 的通项公式;
的通项公式;
(Ⅱ)等差数列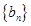 的各项为正,其前
的各项为正,其前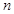 项和为
项和为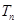 ,且
,且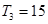 ,又
,又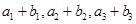 成等比数列,求
成等比数列,求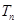 .
.
(执信中学、中山纪念中学、深圳外语)三校联考 09.02
一.选择题:
二.填空题:9.1;
10.15;
11.


13. ;
14.
;
14. ;
15.
;
15. .
.
三.解答题:
16.(1) =
= =
= 2分
2分
= =
= 4分
4分

 6分
6分
(2) =
= =
=
= =
= 9分
9分
由 ,得
,得 10分
10分

 11分
11分
 当
当 , 即
, 即 时,
时, 12分
12分
17.(1)由已知, 的取值为
的取值为 .
2分
.
2分
 ,
,  ,
,
 ,
,  8分
8分

7
8
9
10





 的分布列为:
的分布列为:
9分
(2) 11分
11分
 12分
12分
18.(1)由 .且
.且 得
得 2分
2分
 ,
,
 4分
4分
在 中,令
中,令 得
得 当
当 时,T
时,T =
=
 ,
,
两式相减得 ,
, 6分
6分
 .
8分
.
8分
(2) ,
9分
,
9分
 ,
, , 10分
, 10分
 =2
=2
= ,
13分
,
13分
 14分
14分
19、(Ⅰ)在梯形 中,
中, ,
,


 四边形
四边形 是等腰梯形,
是等腰梯形,
且

 2分
2分
又 平面
平面 平面
平面 ,交线为
,交线为 ,
,
 平面
平面 4分
4分
(Ⅱ)解法一、当 时,
时, 平面
平面 ,
5分
,
5分
在梯形 中,设
中,设 ,连接
,连接 ,则
,则 6分
6分
 ,而
,而
 ,
7分
,
7分
 ,
, 四边形
四边形 是平行四边形,
是平行四边形, 8分
8分
又 平面
平面 ,
, 平面
平面
 平面
平面 9分
9分
解法二:当 时,
时, 平面
平面 ,
,
由(Ⅰ)知,以点 为原点,
为原点, 所在直线为坐标轴,建立空间直角坐标系, 5分
所在直线为坐标轴,建立空间直角坐标系, 5分
 则
则 ,
, ,
, ,
, ,
,
 ,
,
 平面
平面 ,
,

 平面
平面

 与
与 、
、 共面,
共面,
|