
题目列表(包括答案和解析)
设直线 与平面
与平面 相交但不垂直,则下列说法中正确的是
相交但不垂直,则下列说法中正确的是
A.在平面 内有且只有一条直线与直线
内有且只有一条直线与直线 平行
平行
B.过直线 有且只有一个平面与平面
有且只有一个平面与平面 平行
平行
C.与直线 平行的直线可能与平面
平行的直线可能与平面 垂直
垂直
D.与直线 垂直的平面不可能与平面
垂直的平面不可能与平面 平行
平行
设直线 与平面
与平面 相交但不垂直,则下列说法中正确的是
相交但不垂直,则下列说法中正确的是
A.在平面 内有且只有一条直线与直线
内有且只有一条直线与直线 垂直
垂直
B.过直线 有且只有一个平面与平面
有且只有一个平面与平面 垂直
垂直
C.与直线 垂直的直线不可能与平面
垂直的直线不可能与平面 平行
平行
D. 与直线 平行的平面不可能与平面
平行的平面不可能与平面 垂直
垂直
设直线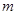 与平面
与平面 相交但不垂直,则下列说法中正确的是 ( )
相交但不垂直,则下列说法中正确的是 ( )
A.在平面 内有且只有一条直线与直线
内有且只有一条直线与直线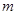 垂直
垂直
B.过直线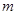 有且只有一个平面与平面
有且只有一个平面与平面 垂直
垂直
C.过直线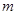 垂直的直线不可能与平面
垂直的直线不可能与平面 平行
平行
D.与直线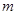 平行的平面不可能与平面
平行的平面不可能与平面 垂直
垂直
设直线 与平面
与平面 相交但不垂直,则下列说法中正确的是
相交但不垂直,则下列说法中正确的是
A.在平面 内有且只有一条直线与直线
内有且只有一条直线与直线 垂直
垂直
B.过直线 有且只有一个平面与平面
有且只有一个平面与平面 垂直
垂直
C.与直线 垂直的直线不可能与平面
垂直的直线不可能与平面 平行
平行
D.与直线 平行的平面不可能与平面
平行的平面不可能与平面 垂直
垂直
A.在平面![]() 内有且只有一条直线与直线
内有且只有一条直线与直线![]() 垂直
垂直
B.过直线![]() 有且只有一个平面与平面
有且只有一个平面与平面![]() 垂直
垂直
C.与直线![]() 垂直的直线不可能与平面
垂直的直线不可能与平面![]() 平行
平行
D.与直线![]() 平行的平面不可能与平面
平行的平面不可能与平面![]() 垂直
垂直
一、选择题(每小题5分,共50分)

二、填空题(每小题4分,共28分)

三、解答题
18.解:(Ⅰ)由已有



(4分)

(6分)
(Ⅱ)由(1) 且
且 (8分)
(8分)
所以 (10分)
(10分)
 (12分)
(12分)

 (14分)
(14分)
19.解:(Ⅰ)同学甲同学恰好投4次达标的概率 (4分)
(4分)
(Ⅱ) 可取的值是
可取的值是
 (6分)
(6分)
 (8分)
(8分)
 (10分)
(10分)
 的分布列为
的分布列为

3
4
5



(12分)
所以 的数学期望为
的数学期望为 (14分)
(14分)
20.解:(Ⅰ)∵PA⊥底面ABCD,BC 平面AC,∴PA⊥BC
平面AC,∴PA⊥BC
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC (4分)
(Ⅱ)取CD的中点E,则AE⊥CD,∴AE⊥AB,又PA⊥底面ABCD,∴PA⊥AE
建立如图所示空间直角坐标系,则
A(0,,0,0),P(0,0, ),C(
),C( ,0),D(
,0),D( ,0)
,0)

 ,
, ,
, (6分)
(6分)
易求 为平面PAC的一个法向量.
为平面PAC的一个法向量.
 为平面PDC的一个法向量
(9分)
为平面PDC的一个法向量
(9分)
∴cos
故二面角D-PC-A的正切值为2. (11分)
(Ⅲ)设 ,则
,则
 ,
,
解得点 ,即
,即 (13分)
(13分)
由 得
得 (不合题意舍去)或
(不合题意舍去)或
所以当 为
为 的中点时,直线
的中点时,直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 (15分)
(15分)
21.解:(Ⅰ)设直线 的方程为:
的方程为:
由 得
得 ,所以
,所以 的方程为
的方程为 (4分)
(4分)
由 得
得 点的坐标为
点的坐标为 .
.
可求得抛物线的标准方程为 .
(6分)
.
(6分)
(Ⅱ)设直线 的方程为
的方程为 ,代入抛物线方程并整理得
,代入抛物线方程并整理得 (8分)
(8分)
设 则
则
设 ,则
,则



 (11分)
(11分)
当 时上式是一个与
时上式是一个与 无关的常数.
无关的常数.
所以存在定点 ,相应的常数是
,相应的常数是 .
(14分)
.
(14分)
22.解:(Ⅰ)当 时
时 (2分)
(2分)
 在
在 上递增,在
上递增,在 上递减
上递减
所以 在0和2处分别达到极大和极小,由已知有
在0和2处分别达到极大和极小,由已知有
 且
且 ,因而
,因而 的取值范围是
的取值范围是 .
(4分)
.
(4分)
(Ⅱ)当 时,
时, 即
即
|