
题目列表(包括答案和解析)
![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()

(A) (B)
(B) (C)
(C) (D)
(D)

(A) (B)
(B) (C)
(C)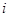 (D)
(D)
一.选择题 (本大题共10小题,每题5分,共50分)
1.C; 2.D; 3,A; 4.B; 5.B;
6.A; 7.B; 8.D; 9.B; 10.D;
二.填空题 (本大题共7小题,每题4分,共28分)
11. ; 12.
; 12. ,
, ;
;
 .
. ; 14.
; 14. ,
, ; 15.
; 15. ; 16.
; 16. ; 17.
; 17. .
.
三.解答题 (本大题共5小题,第18―20题各14分,第21、22题各15分,共72分)
18.解:(1)因为 ,所以
,所以 ,…………3分
,…………3分
得 ,
,
所以 …………………………………3分
…………………………………3分
(2)由 得
得 ,…………………………………2分
,…………………………………2分
 ……………………2分
……………………2分
 ………………………………4分
………………………………4分
19.解:(1) …………………2分
…………………2分
当 时,
时, …………………2分
…………………2分
∴ ,即
,即
∴ 是公比为3的等比数列…………………2分
是公比为3的等比数列…………………2分
(2)由(1)得: …………………2分
…………………2分
设 的公差为
的公差为 (
( ), ∵
), ∵ ,∴
,∴ ………………2分
………………2分
依题意有 ,
, ,
,
∴
 ,得
,得 ,或
,或 (舍去)………………2分
(舍去)………………2分
故 ………………2分
………………2分
20.解(1) 面
面 ,
,
由三视图知:侧棱 面
面 ,
, ,
,
∴
∴ 面
面 ………………2分
………………2分
∴ ,又
,又 ,∴
,∴ ①………………2分
①………………2分
∵ 为正方形,∴
为正方形,∴ ,又
,又
∴ ②………………2分
②………………2分
由①②知 平面
平面 ………………2分
………………2分
(2)取 的中点
的中点 ,连结
,连结 ,
, ,由题意知
,由题意知 ,∴
,∴
由三视图知:侧棱 面
面 ,∴平面
,∴平面 平面
平面
∴ 平面
平面
∴ 就是
就是 与面
与面 所成角的平面角………………3分
所成角的平面角………………3分
 ,
, 。故
。故 ,又正方形
,又正方形 中
中
在 中,∴
中,∴ ,∴
,∴
∴ ………………3分
………………3分
综上知 与面
与面 所成角的大小的余弦值为
所成角的大小的余弦值为
21.解(1)当 ,
, 时,
时, ,………………1分
,………………1分
 ………………2分
………………2分
∴当 时
时 ,此时
,此时 为减函数,………………1分
为减函数,………………1分
当 时
时 ,些时
,些时 为增函数………………1分
为增函数………………1分
由 ,
,
当 时,求函数
时,求函数 的最大值
的最大值 ………………2分
………………2分
(2) ………………1分
………………1分
①当 时,在
时,在 上
上 ,
, ,
,
∵ 在
在 上为减函数,∴
上为减函数,∴ ,则
,则
 或
或 得
得 ………………3分
………………3分
②当 时,
时,

∵ 在
在 上为减函数,则
上为减函数,则
∵ 在
在 上为增函数,在
上为增函数,在 上为减函数,在
上为减函数,在 上为增函数,则
上为增函数,则
 得
得 又
又 ,∴
,∴ ………………3分
………………3分
综上可知, 的取值范围为
的取值范围为 ………………1分
………………1分
22.(1)记A点到准线距离为 ,直线
,直线 的倾斜角为
的倾斜角为 ,
,
由抛物线的定义知 ,………………………2分
,………………………2分
∴ ,
,
∴ ………………………3分
………………………3分
(2)设 ,
, ,
,
由 得
得 ,………………………2分
,………………………2分
由 得
得 且
且
 ,同理
,同理 ……………………2分
……………………2分
由 得
得 ,…………………………2分
,…………………………2分
即: ,
,
∴ ,…………………………2分
,…………………………2分
 ,得
,得 且
且 ,
,
由 且
且 得,
得,
 的取值范围为
的取值范围为 …………………………2分
…………………………2分
命题人
吕峰波(嘉兴) 王书朝(嘉善) 王云林(平湖)
胡水林(海盐) 顾贯石(海宁) 张晓东(桐乡)
吴明华、张启源、徐连根、洗顺良、李富强、吴林华
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com