
题目列表(包括答案和解析)
 (3)当△OPQ∽△ABP时,抛物线y=
(3)当△OPQ∽△ABP时,抛物线y= x2+bx+c经过B、P两点,求抛物线的解析式;
x2+bx+c经过B、P两点,求抛物线的解析式; 轴的平
轴的平 的三个顶点
的三个顶点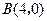 、
、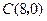 、
、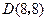 .抛物线
.抛物线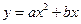 过
过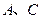 两点.
两点.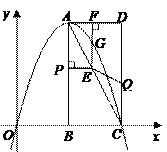
 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式; 从点
从点 出发,沿线段
出发,沿线段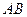 向终点
向终点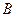 运动,同时点
运动,同时点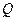 从点
从点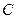 出发,沿线段
出发,沿线段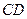 向终点
向终点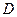 运动,速度均为每秒1个单位长度,运动时间为
运动,速度均为每秒1个单位长度,运动时间为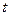 秒.过点
秒.过点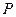 作
作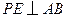 交
交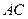 于点
于点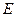 .
.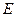 作
作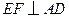 于点
于点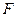 ,交抛物线于点
,交抛物线于点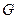 .当
.当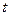 为何值时,线段
为何值时,线段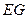 最长?
最长?(本小题满分12分)
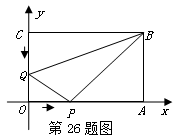
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA="16" cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒2cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用含t的式子表示△OPQ的面积S;
(2)判断四边形OPBQ的面积是否是一个定值,如果是,请求出这个定值;如果不是,请说明理由;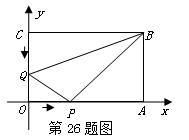 (3)当△OPQ∽△ABP时,抛物线y=
(3)当△OPQ∽△ABP时,抛物线y=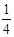 x2+bx+c经过B、P两点,求抛物线的解析式;
x2+bx+c经过B、P两点,求抛物线的解析式;
(4)在(3)的条件下,过线段BP上一动点M作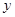 轴的平
轴的平
行线交抛物线于N,求线段MN的最大值.
(本小题满分12分)如图,在平面直角坐标系中,已知矩形 的三个顶点
的三个顶点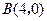 、
、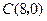 、
、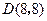 .抛物线
.抛物线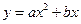 过
过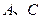 两点.
两点.
(1)直接写出点 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式;
(2)动点 从点
从点 出发,沿线段
出发,沿线段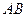 向终点
向终点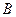 运动,同时点
运动,同时点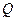 从点
从点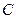 出发,沿线段
出发,沿线段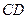 向终点
向终点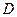 运动,速度均为每秒1个单位长度,运动时间为
运动,速度均为每秒1个单位长度,运动时间为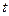 秒.过点
秒.过点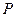 作
作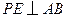 交
交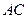 于点
于点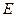 .
.
过点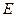 作
作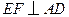 于点
于点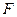 ,交抛物线于点
,交抛物线于点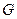 .当
.当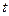 为何值时,线段
为何值时,线段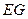 最长?
最长?
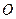 和
和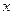 轴上另一点
轴上另一点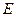 ,顶点
,顶点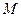 的坐标为
的坐标为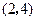 ;矩形
;矩形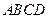 的顶点
的顶点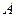 与点
与点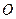 重合,
重合,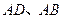 分别在
分别在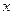 轴、
轴、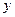 轴上,且
轴上,且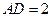 ,
,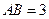 .
. 以每秒1个单位长度的速度从图1所示的位置沿
以每秒1个单位长度的速度从图1所示的位置沿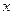 轴的正方向匀速平行移动,同时一动点
轴的正方向匀速平行移动,同时一动点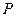 也以相同的速度从点
也以相同的速度从点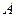 出发向
出发向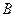 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为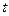 秒(
秒(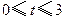 ),直线
),直线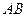 与该抛物线的交点为
与该抛物线的交点为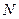 (如图2所示).
(如图2所示).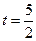 时,判断点
时,判断点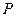 是否在直线
是否在直线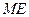 上,并说明理由;
上,并说明理由;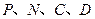 为顶点的多边形面积为
为顶点的多边形面积为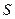 ,试问
,试问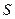 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.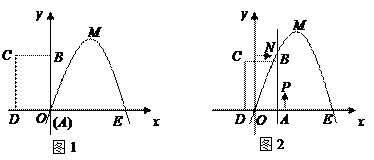
一、1、C;2、C;3、D;4、A;5、C;6、B;7、D;8、B;9、A;10、B;
二、11、8;2、.files/image057.gif) 且
且.files/image059.gif) ;13、
;13、.files/image061.gif) ;14、
;14、.files/image063.gif) 或
或.files/image065.gif) ;
;
15、6;16、六;17、旋转中心和旋转角;18、9:30;19、4;20、5;
.files/image067.jpg) 三、21、原式=
三、21、原式=.files/image069.gif) ;当
;当.files/image071.gif) 时,原式=
时,原式=.files/image073.gif) ;
;
22、如图,易算出AE=
由比例可知:CH=.files/image075.gif)
故影响采光。
23、11,17,59;S=6n-1;
24、(1)y=―x2+2x+3;(2)x=1,M(1,4),(3)9;
25、(1)相同点:甲台阶与乙台阶的各阶高度参差不齐,不同点:甲台阶各阶高度的极差比乙台阶小;
(2)甲台阶,因为甲台阶各阶高度的方差比乙台阶小;
(3)使台阶的各阶高度的方差越小越好。
26、(1)r=3;(2)3<r<4;(3)r=4或5;(4)r>4且r≠5;
27、(1)a=110,b=90;提示:可由.files/image077.gif) 解得;
解得;
(2)从表中的信息可知:该农户每年新增林地亩数的增长率为30%,
则2004年林地的亩数为26×(1+30%)=33.8亩,
2005年林地的亩数为33.8×(1+30%)=43.94亩,
.files/image079.jpg) 故2005年的总收入为2000+43.94×110+33.8×90=8775.4元。
故2005年的总收入为2000+43.94×110+33.8×90=8775.4元。
28、(1)P(摸到红球)= P(摸到同号球)=.files/image081.gif) ;故没有利;
;故没有利;
(2)每次的平均收益为.files/image083.gif) ,
,
故每次平均损失.files/image085.gif) 元。
元。
29、.files/image087.gif) cm;提示:由r=20cm,h=20
cm;提示:由r=20cm,h=20.files/image089.gif) cm,可得母线l=80cm,而圆锥侧面展开后的扇形的弧长为
cm,可得母线l=80cm,而圆锥侧面展开后的扇形的弧长为.files/image091.gif) ,可求得圆锥侧面展开后的扇形的圆心角为900,故最短距离为80
,可求得圆锥侧面展开后的扇形的圆心角为900,故最短距离为80.files/image087.gif) cm。
cm。
30、(1)(6―x , .files/image032.gif) x );
x );
(2)设ㄓMPA的面积为S,
在ㄓMPA中,MA=6―x,MA边上的高为.files/image032.gif) x,其中,0≤x≤6.
x,其中,0≤x≤6.
∴S=.files/image094.gif) (6―x)×
(6―x)×.files/image032.gif) x=
x=.files/image096.gif) (―x2+6x)
= ―
(―x2+6x)
= ― .files/image096.gif) (x―3)2+6
(x―3)2+6
∴S的最大值为6, 此时x =3. (3)延长NP交x轴于Q,则有PQ⊥OA
①若MP=PA ∵PQ⊥MA ∴MQ=QA=x. ∴3x=6, ∴x=2;
②若MP=MA,则MQ=6―2x,PQ=.files/image032.gif) x,PM=MA=6―x
x,PM=MA=6―x
在RtㄓPMQ
中,∵PM2=MQ2+PQ2 ∴(6―x) 2=(6―2x) 2+
(.files/image032.gif) x) 2
x) 2
∴x=.files/image099.gif)
③若PA=AM,∵PA=.files/image101.gif) x,AM=6―x
x,AM=6―x
∴.files/image101.gif) x=6―x ∴x=
x=6―x ∴x=.files/image104.gif)
综上所述,x=2,或x=.files/image099.gif) ,或x=
,或x=.files/image104.gif) 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com