
题目列表(包括答案和解析)
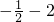 =________.
=________. =________.
=________.| 3 | 2 |


一、1.A 2. C 3. D 4. D 5. B 6.D 7. A 8. A 9. B 10. B 11. D 12. B 13. C 14. D 15. A
二、16.±3 17..files/image220.gif) 18.
18..files/image222.gif) 19.矩形、圆
19.矩形、圆 .files/image086.gif)
三、22.解原式=.files/image225.gif)
23、解设.files/image227.gif) 原方程可化为
原方程可化为.files/image229.gif) 。解得
。解得.files/image231.gif)
.files/image233.gif)
当.files/image235.gif) 解得
解得.files/image237.gif)
.files/image239.gif) 解得
解得.files/image241.gif)
经检验.files/image243.gif)
.files/image245.gif) 是原方程的根。
是原方程的根。
24、∵AC∥BD ∴∠C=∠D ∠CAO=∠DBO AO=BO ∴△AOC≌△BOD
∴CO=DO ∵E、F分别是OC、OD的中点 ∴OF=.files/image002.gif) OD=
OD=.files/image002.gif) OC=OE 。
OC=OE 。
由AO=BO、EO=FO ∴四边表AFBE是平等四边形。
25、解由图象可行.files/image248.gif) 是
是.files/image250.gif) 的反比例函数设
的反比例函数设.files/image252.gif) 经过A(2,18)
经过A(2,18)
.files/image254.gif) ∴函数表达式为:
∴函数表达式为:.files/image248.gif) =
=.files/image256.gif) 。
。
26、(1)设该船厂运输x年后开始盈利,72x-(120+40x)?0,x?.files/image258.gif) ,
,
因而该船运输4年后开始盈利。(2).files/image260.gif) (万元)。
(万元)。
四、27、(1)不合格 (2)80名
(3)合理,理由,利用样本的优秀人数来诂计总体的优秀人数。
五、28、作AD⊥BC交BC延长线于D,设AD=.files/image029.gif) ,在Rt△ACD中,∠CAD=30°
,在Rt△ACD中,∠CAD=30°
∴CD=.files/image263.gif) 。在Rt△ABD中,∠ABD=30°∴BD=
。在Rt△ABD中,∠ABD=30°∴BD= .files/image265.gif)
∵BC=8 .files/image267.gif)
.files/image269.gif) ∴有触礁危险。
∴有触礁危险。
六29、解:(1)△.files/image271.gif) 。证明:
。证明:.files/image273.gif) 。
。
又.files/image275.gif)
(2).files/image277.gif) 理由:
理由:.files/image279.gif) 。
。
又.files/image281.gif) ∽
∽.files/image283.gif) ,即
,即.files/image285.gif) 。
。
七、30.解(1)等腰直角三角形 (2)当.files/image287.gif) J 等边三角形。
J 等边三角形。
证明;连结.files/image289.gif) 是⊙
是⊙.files/image098.gif) 的切线
的切线
.files/image292.gif)
.files/image294.gif)
.files/image296.gif) 又
又 .files/image298.gif) 是等边三角形。(3)等腰三角形。
是等边三角形。(3)等腰三角形。
八 31.(1)作图略 (2).files/image300.gif)
九 32.(1)1140≤45x+75(20-x)≤1170 (2)11≤x≤12
∵x为正整数∴当x=11时,20-11=9当=12时20-12=8
∴生产甲产品11件,生产乙产品9件或 生产甲产品12件,生产乙产品8件。
十 33.解:(1)∵DQ//AP,∴当AP=DQ时,四边形APQD是平行四边形。
此时,3t=8-t。解得t=2(s)。即当t为2s时,四边形APQD是平行四边形。
(2)∵⊙P和⊙Q的半径都是
而当PQ=
①当 四边形APQD是平行四边形时,由(1)得t=2(s)。
② 当 四边形APQD是等腰梯形时,∠A=∠APQ。
∵在等腰梯形ABCD中,∠A=∠B,∴∠APQ=∠B。∴PQ//BC。
∴四边形PBCQ平行四边形 。此时,CQ=PB。∴t=12-3t。解得t3(s)。
综上,当t为2s或3s时,⊙P和⊙Q相切。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com