
题目列表(包括答案和解析)
从2004年开始,某市政府准备在市区实施“景观工程”,以现有平顶的民用多层住宅进行“平改坡”,计划将平顶房屋改为尖顶,并铺上彩色瓦片,现对某幢房屋有如下两种改造方案:
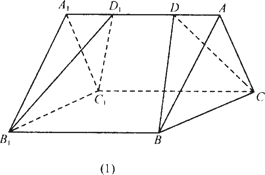
方案一:坡顶如图(1)所示,为顶面是等腰三角形的直三棱柱,尖顶屋脊![]() 与房屋长度
与房屋长度![]() 等长,有两个坡面需铺上瓦片.
等长,有两个坡面需铺上瓦片.
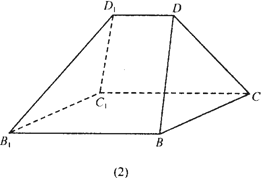
方案二:坡顶如图(2)所示,为由(1)削去两端相同的两个三棱锥而得,尖顶屋脊![]() 比房屋长度
比房屋长度![]() 要短,有四个坡面需铺上瓦片.
要短,有四个坡面需铺上瓦片.
若房屋长度![]() ,宽BC=2b,屋脊高为h,试问哪种方案尖顶铺设的瓦片比较省?说明理由.
,宽BC=2b,屋脊高为h,试问哪种方案尖顶铺设的瓦片比较省?说明理由.

(2)一条直线和一个平面相交,但不______时,这条直线就叫做这个平面的_______,斜线与平面的交点叫做_____.从平面外一点向平面引斜线,这点与________间的线段叫做这点到这个平面的_______.如图所示,直线PR∩α=R,PR不______于α,直线PR是α的一条_____,点R为_______,线段_____是点P到α的______.?
(3)平面外一点到这个平面的垂线段______条,而这点到这个平面的______有无数条.?
(4)从斜线上斜足以外的一点向平面引垂线,过垂足的直线叫做斜线在这个平面内的_______,________与________间的线段叫做这点到平面的斜线段在这个平面内的________.如图所示,直线_____是直线PR在平面α上的______,线段______是点P到平面α的斜线段PR在平面α上的射影.?
(5)斜线上任意一点在平面上的射影一定在斜线的_____上.事实上,设a是平面α的斜线,B为斜足,在a上任取一点A,作AA1⊥α,A1是垂足,则A1、B确定的直线a′是a在平面α内的______,如图所示,设P是a上任意一点,在a和AA1确定的平面内,作PP1∥AA1,PP1必与a′相交于一点P1.∵AA1α__________ ,PP1______________AA1,∴PP1__________α.P1为P在平面α上的射影,所以点P在平面α上的射影一定在直线a在平面α上的射影a′上.

如图,在三棱锥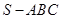 中,平面
中,平面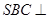 平面
平面 ,
,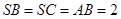 ,
,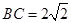 ,
,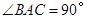 ,
,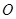 为
为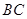 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角 的余弦值.
的余弦值.

【解析】第一问中利用因为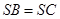 ,
,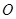 为
为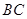 中点,所以
中点,所以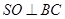
而平面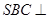 平面
平面 ,所以
,所以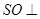 平面
平面 ,再由题设条件知道可以分别以
,再由题设条件知道可以分别以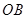 、
、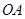 、
、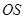 为
为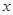 ,
,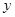 ,
,
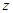 轴建立直角坐标系得
轴建立直角坐标系得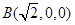 ,
,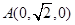 ,
,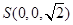 ,
,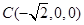 ,
,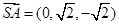 ,
,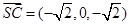 ,
,
故平面 的法向量
的法向量 而
而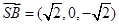 ,故点B到平面
,故点B到平面 的距离
的距离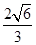
第二问中,由已知得平面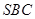 的法向量
的法向量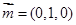 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于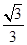
解:(Ⅰ)因为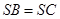 ,
,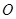 为
为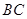 中点,所以
中点,所以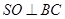
而平面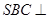 平面
平面 ,所以
,所以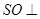 平面
平面 ,
,
再由题设条件知道可以分别以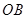 、
、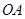 、
、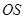 为
为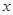 ,
,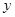 ,
,
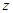 轴建立直角坐标系,得
轴建立直角坐标系,得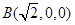 ,
,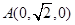 ,
,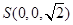 ,
,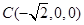 ,
,
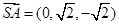 ,
,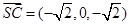 ,故平面
,故平面 的法向量
的法向量
而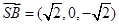 ,故点B到平面
,故点B到平面 的距离
的距离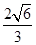
(Ⅱ)由已知得平面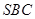 的法向量
的法向量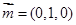 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于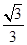
如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求证: ;
;
(III)设PD=AD=a, 求三棱锥B-EFC的体积.

【解析】第一问利用线面平行的判定定理, ,得到
,得到
第二问中,利用
 ,所以
,所以
又因为 ,
, ,从而得
,从而得
第三问中,借助于等体积法来求解三棱锥B-EFC的体积.
(Ⅰ)证明:
 分别是
分别是 的中点,
的中点, 
 ,
, . …4分
. …4分
(Ⅱ)证明: 四边形
四边形 为正方形,
为正方形, .
.
 ,
,  .
.
 ,
,  ,
,
 .
. ,
, . ………8分
. ………8分
(Ⅲ)解:连接AC,DB相交于O,连接OF, 则OF⊥面ABCD,
∴

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com