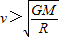
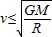
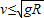
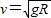
一行星质量为M，半径是R，表面的重力加速度是g．卫星绕它做匀速圆周运动的速率是v，若万有引力恒量为G，则（ ）
A．
B．
C．
D．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

题号

1

2

3

4

5

6

7

8

9

10

11

答案

B

C

D

D

B

C

AC

AD

BC

BD

BC

12．（1）1.00kΩ。将选择开关打到“×100”挡；将两表笔短接，调节调零旋钮，进行欧姆挡调零；再将被电阻接到两表笔之间测量其阻值并读出读数；测量完毕将选择开关打到“OFF”挡。（2）见右图。（3）大于。

13．（1）2L/t²；不改变；无关；9.8m/s²；a=gsinα；（2）控制变量法。

14．解：（1）N==；

（2）U₁=220V，U₂<=11000V，>。

15．解：（1）设光进入玻璃管的入射角为θ，射向内表面的折射角为β，据折射定律有：

sinα=nsinθ；sinβ≥1/n；

据正弦定律有：2sinθ/d= sinβ/d；解得：sinα≥1/2；所以：α≥30°。

（2）有三处，第一处，60°；第二处，180°；第三处，60°。

16．解：（1）钍核衰变方程                     ①

（2）设粒子离开电场时速度为，对加速过程有

                                       ②

     粒子在磁场中有                               ③

     由②、③得                         ④

（3）粒子做圆周运动的回旋周期

                                                     ⑤

     粒子在磁场中运动时间                                   ⑥

     由⑤、⑥得                         ⑦

17．解：（1）当绳被拉直时，小球下降的高度h=Lcosθ-d=0.2m

据h=gt²/2，可得t=0.2s，所以v₀=Lsinθ/t=4m/s

（2）当绳被拉直前瞬间，小球竖直方向上的速度v_y=gt=2m/s，绳被拉直后球沿绳方向的速度立即为零，沿垂直于绳方向的速度为v_t= v₀cos53º- v_ysin53º=0.8m/s，垂直于绳向上。

此后的摆动到最低点过程中小球机械能守恒：

在最低点时有：

代入数据可解得：T＝18.64N

18．解：（1）a方向向下时，mg－BIL=ma，I= ，Q=，

解得：Q=；

a方向向上时，BIL－mg=ma，I= ，Q=，

解得：Q=；

（2）a方向向下时，据动量定理，有：

mgt－BLt₂=mv－0，=，解得：t=；

a方向向上时，同理得：t=

19．解：（1）AB第一次与M碰后　A返回速度为v₀，m_Av₀=(m_A+m_B)v₁，解得v₁=4m/s；

（2）A相对B滑行Δs₁，μm_AgΔs₁=－，解得Δs₁=6m；

（3）AB与N碰撞后，返回速度大小为v₁，B与M再相碰后停止，设A与M再碰时的速度为v₂，－μm_AgΔs₁=－，解得v₂=2m/s，

A与M碰后再与B速度相同时为v₃，相对位移Δs₂，m_Av₂=(m_A+m_B)v₃，v₃=

μm_AgΔs₂=－，解得：Δs₂= ，……，最终A和B停在M处，

Δs =Δs₁+Δs₂+……=13.5m。