查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

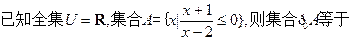
A．{x|x＜-1或x＞2}	B．{x|x≤-1或x＞2}
C．{x|x＜-1或x≥2}	D．{x|x≤-1或x≥2}

查看答案和解析>>

查看答案和解析>>

第Ⅰ卷

一、选择题：本大题共12小题，每小题5分，共60分.

题号

1

2

3

4

5

6

7

8

9

10

11

12

答案

C

文A

理D

A

D

C

D

A

文C

理B

A

B

D

文C

理C

第II卷

二、填空题：本大题共4小题，每小题5分，共20分.

14.(理)3  （文）    14.2         15.       16. ③④

三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.

17．本小题满分10分

解：(Ⅰ)∵m⊥n，

       ∴m?n=(,cosA+1)?(sinA,－1)=sinA－(cosA+1)=0，

       ∴sinA－cosA=1，………………………………………………………………2分

       ∴sin(A－)=．…………………………………………………………………3分

       ∵0<A<p，∴，∴，………………………………5分

       ∴A=．……………………………………………………………………………6分

       (Ⅱ)在△ABC中，A=，a=2，cosB=，

       ∴sinB=．……………………………………………7分

       由正弦定理知：，…………………………………………………8分

       ∴b=，∴b=．……………………………………10分

18．(本小题满分12分)

解：（1）由甲射手命中目标的概率与距离的平方成反比，可设，

∵，∴，   ………………………………………    2分

∴，. ………………………………………………   4分

∴，.……………………………  6分

（2）（理）的所有可能取值为0，1，2，3.

, ……………………………   7分

，  …………………………………  8分

，  ……………………………………………   9分

.   ……………………………………………………………  10分

∴. …………………… 12分

（文）记“射手甲在该射击比赛中能得分”为事件A，则

，……………………  9分

∴. ………………………… 12分

19．(本小题满分12分)

解：(Ⅰ)证明：连接AC₁，设AC₁∩A₁C=E，连接DE．………………1分

∵A₁B₁C₁―ABC是直三棱柱，且AC=AA₁=，

∴AA₁C₁C是正方形，E是AC₁中点，

又D为AB中点，∴ED∥BC₁．……………………………………3分

又EDÌ平面A₁CD，BC₁Ë平面A₁CD，

∴BC₁∥平面A₁CD．…………………………………………………4分

(Ⅱ)解法一：设H是AC中点，F是EC中点，连接DH，HF，FD．……5分

∵D为AB中点， ∴DH∥BC，同理可证HF∥AE，又AC⊥CB，故DH⊥AC．

又侧棱AA₁⊥平面ABC，

∴AA₁⊥DH，      ∴DH⊥平面AA₁C₁C．…………………7分

由(Ⅰ)得AA₁C₁C是正方形，则A₁C⊥AE，∴A₁C⊥HF．

∵HF是DF在平面AA₁C₁C上的射影，∴DF⊥A₁C．

∴∠DFH是二面角A―A₁C―D的平面角．…8分

又DH=，HF=．…10分

∴在直角三角形DFH中，tan∠DFH=．…11分

∴二面角A―A₁C―D的大小为arctan．……………………12分

解法二：在直三棱柱A₁B₁C₁―ABC中，∵AC⊥CB，∴分别以CA，CB，CC₁所在的直线为x轴，y轴，z轴建立如图所示空间直角坐标系C?xyz．因为BC=1，AA₁=AC=，则

C(0,0,0)，A(,0,0)，B(0,1,0)，D，…………5分

设平面A₁DC的法向量为n=(x,y,z)，则

       ，       …………………………6分

∵=，=(,0,)，

∴ ，则．…7分

取x=1，得平面A₁DC的一个法向量为n=(1,－,－1)，…………9分

m==(0,1,0)为平面CAA₁C₁的一个法向量．………………………10分

cos<m?n>=．………………………………11分

由图可知，二面角A―A₁C―D的大小为arccos．………………12分

20．(本小题满分12分)

解：(Ⅰ)∵a_n+1= f()=．…………………………3分

∴{a_n}是以为公差的等差数列．

又a₁=1，∴a_n=．  ………………………………………(理)5分(文)6分

(Ⅱ) (理)当n≥2时，，

又b₁==，

∴S_n=b₁+b₂+???+b_n=．…8分

∵S_n<，对nÎN^*成立．

∵关于n递增，且当n®+∞时，及，

∴，m≥2009．∴最小正整数m=2009．………………………12分

（文）T_n=a₂(a₁－a₃)+a₄(a₃－a₅)+???+a_2n(a_2n-1－a_2n+1)

=－(a₂+a₄+???+a_2n) ………………………………………………8分

=．…………………………………12分

21．(本小题满分12分)

解：(Ⅰ)由得(a²+b²)x²－2a²x+a²－a²b²=0，…………………2分

设A(x₁，y₁)、B(x₂，y₂)，AB中点为M(x₀，y₀)．

∴x₁+x₂=，x₀=，y₀=－x₀+1=，……………………4分

∴M(，)，代入x－2y=0

得a²=2b²，∴，……………………………………………………5分

∴e=．………………………………………………………6分

(Ⅱ)由(Ⅰ)知椭圆方程可化为， ……………………………7分

所以右焦点F₂(b，0)关于直线l：x－2y=0的对称点F₂′(b，b)，……9分

将其代入x²+y²=4，得(b)²+(b)²=4，∴b²=4．…………………………10分

所以椭圆的方程为．…………………………………………12分

22．(本小题满分12分)

解：(理)(Ⅰ) f′(x)=－，∵x≥1，∴lnx≥0，∴f′(x)≤0，故f(x)在[1,+∞)递减．……4分

(Ⅱ) f(x)≥Û≥k，记g(x)=，

       则g′(x)=．…………………………5分

       再令h(x)=x－lnx，则h′(x)=1－．

       ∵x≥1，∴h′(x)≥0，∴h(x)在[1,+∞)上递增………………………………………6分

       ∴[h(x)]_min=h(1)=1>0，从而g′(x)>0，故g(x)在[1,+∞)上也单调递增． ………7分

       ∴[g(x)]_min=g(1)=2，∴k≤2．………………………………………………………8分

       (Ⅲ)证法1：用数学归纳法，略

       证法2：由(Ⅱ)知：f(x)≥恒成立，即．

       令x=n(n+1)，则，………………………………9分

∴，，，…，

，……………………………………………………10分

将以上不等式相加得：

．……………………………………12分

(文)解：(Ⅰ )由f(x)=x³+ax²+bx+c，求导数得f′(x)=3x²+2ax+b．…………1分

过y=f(x)上的点P(1，f(1))的切线方程为：y－f(1)=f′(1)(x－1)，

即y－(a+b+c+1)=(3+2a+b)(x－1)．…………………………………………3分

而过y=f(x)上的点P(1，f(1)) 的切线方程为y=3x+1，

故即…………………………………………4分

∵f(x)在x=－2处有极值，故f′(－2)=0，∴－4a+b=－12，③……………5分

由①②③得a=2，b=－4，c=5．

∴f(x)=x³+2x²－4x+5．…………………………………………………………6分

(Ⅱ )解法一：y=f(x)在[－2,1]上单调递增，又f′(x)=3x²+2ax+b，由①知2a+b=0．

依题意f′(x)在[－2,1]上恒有f′(x)≥0，即3x²－bx+b≥0．……………………8分

①当x=≥1时，f′(x)_min=f′(1)=3－b+b>0，∴b≥6；………………………9分

②当x=≤－2时，f′(x)_min=f′(－2)=12+2b+b≥0，∴bÎÆ；………………10分

③当－2≤≤1时，f′(x)_min=≥0，则0≤b≤6．………………………11分

综上所述，参数b的取值范围是[0,+∞)．……………………………………12分

解法二：同)解法一，可得3x²-bx+b≥0．………………………………………8分

即b(x－1)≤3x²．

当x=1时，不等式显然成立．

当x≠1时，x－1<0，∴b≥．……………………………………………10分

∵=3(x－1)++6≤－6+6=0，

∴b≥0．…………………………………………………………………………12分

数学既重基础又突出考查主线

西北师大附中高级教师 李树林

　　  试卷点评:本试卷题型配置合理，考查知识点覆盖全面,试题严谨准确，无科学性知识性错误。思维量、计算量适中。更值得一提的是试卷平和温馨，无偏题怪题，既重基础又突出考查主线，学生倍感亲切。这既对后期复习具有良好的导向作用，尤其是对稳定学生情绪，鼓舞士气发挥重要作用。总之，本试卷与近年高考题相比更接近。如果多出现一些创新题将更能体现课改精神。另外，应加大压轴题的分量，特别是21题分量明显不足。

　　  复习建议:合理定位，“量身”制定复习方案。后期复习对自己恰当定位很重要。夺三甲、进前十、奔名校、够重点、上普本，一定要有自己的具体目标要求。你在什么层面，就要进行相对应的复习。既敢追求又能舍弃。基础未过关的，宁可再打基础也要舍弃综合性的问题，想拔高的就要对一些“尖端”问题猛攻。

　　  力所能及地做好专题复习。首先做好6个方向的专题复习：向量与三角问题专题、向量与立体几何问题专题、概率与统计问题专题、函数与不等式问题专题、数列与不等式问题专题、解析几何问题专题。建议自己进行专题组卷，比如三角题，将近年三角考题精选十余道组成试卷进行专题练习。其次做好思想方法专题复习。另外，有些典型问题也可以专题题组的方式复习。如分段函数，选择相关题目组成专题卷，内容包括单调性、奇偶性、值域、反函数等等，这样做复习效果倍增。

　　  做好临场训练：关注应试技法，如客观题用画图、检验等特殊方法，特别是选择题要用好选择这一“拐杖”；重视解题程序的训练：如用向量法解立体几何题的步骤、用直译法求轨迹方程的步骤、直线与圆锥曲线问题的求解步骤、解概率题的步骤、画数据的频率分布直方图的步骤、用数学归纳法证明问题的步骤、求线性规划问题的步骤等等；做好答卷规范性的训练:特别是今年实行网上阅卷对答题规范性要求更高，必须及早训练否则一定影响考试效果。