
题目列表(包括答案和解析)
已知等比数列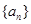 中,
中,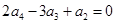 ,且
,且 ,公比
,公比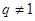 ,(1)求
,(1)求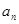 ;(2)设
;(2)设 ,求数列
,求数列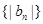 的前
的前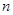 项和
项和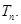
【解析】第一问,因为由题设可知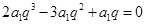
又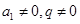 故
故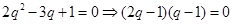
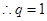 或
或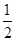 ,又由题设
,又由题设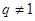
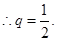 从而
从而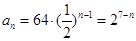
第二问中,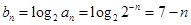
当 时,
时,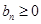 ,
, 时
时
故 时,
时,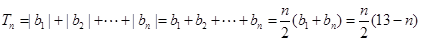
 时,
时,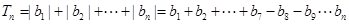
分别讨论得到结论。
由题设可知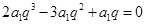
又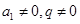 故
故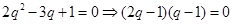
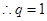 或
或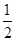 ,又由题设
,又由题设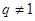
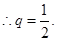
从而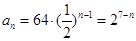 ……………………4分
……………………4分
(2)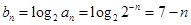
当 时,
时,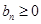 ,
, 时
时 ……………………6分
……………………6分
故 时,
时,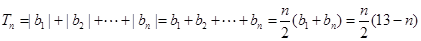 ……8分
……8分
 时,
时,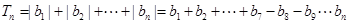
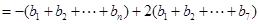
 ……………………10分
……………………10分
综上可得

设数列 的各项均为正数.若对任意的
的各项均为正数.若对任意的 ,存在
,存在 ,使得
,使得 成立,则称数列
成立,则称数列 为“Jk型”数列.
为“Jk型”数列.
(1)若数列 是“J2型”数列,且
是“J2型”数列,且 ,
, ,求
,求 ;
;
(2)若数列 既是“J3型”数列,又是“J4型”数列,证明:数列
既是“J3型”数列,又是“J4型”数列,证明:数列 是等比数列.
是等比数列.
【解析】1)中由题意,得 ,
, ,
, ,
, ,…成等比数列,且公比
,…成等比数列,且公比 ,
,
所以.
(2)中证明:由{ }是“j4型”数列,得
}是“j4型”数列,得 ,…成等比数列,设公比为t. 由{
,…成等比数列,设公比为t. 由{ }是“j3型”数列,得
}是“j3型”数列,得
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 …成等比数列,设公比为
…成等比数列,设公比为 ;
;
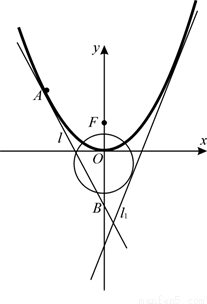
如图,已知直线 (
(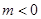 )与抛物线
)与抛物线 :
: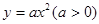 和圆
和圆 :
: 都相切,
都相切, 是
是 的焦点.
的焦点.
(Ⅰ)求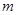 与
与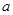 的值;
的值;
(Ⅱ)设 是
是 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点 ,以
,以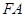 、
、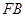 为邻边作平行四边形
为邻边作平行四边形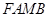 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点 所在的定直线为
所在的定直线为 , 直线
, 直线 与
与 轴交点为
轴交点为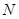 ,连接
,连接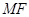 交抛物线
交抛物线 于
于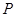 、
、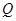 两点,求△
两点,求△ 的面积
的面积 的取值范围.
的取值范围.
【解析】第一问中利用圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去)
舍去)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
,
第二问中,由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形
, ∵四边形FAMB是以FA、FB为邻边作平行四边形
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线
第三问中,设直线 ,代入
,代入 得
得 结合韦达定理得到。
结合韦达定理得到。
解:(Ⅰ)由已知,圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去). …………………(2分)
舍去). …………………(2分)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
, .
……(2分)
.
……(2分)
(Ⅱ)由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形,
, ∵四边形FAMB是以FA、FB为邻边作平行四边形,
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线 上.…(2分)
上.…(2分)
(Ⅲ)设直线 ,代入
,代入 得
得 , ……)得
, ……)得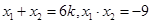 ,
…………………………… (2分)
,
…………………………… (2分)
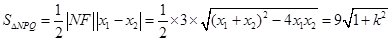 ,
,
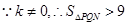 .
. △
△ 的面积
的面积 范围是
范围是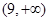
如图,三棱柱 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。

(I) 证明:平面 ⊥平面
⊥平面
(Ⅱ)平面 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题.
【解析】(Ⅰ)由题设知BC⊥ ,BC⊥AC,
,BC⊥AC, ,∴
,∴ 面
面 , 又∵
, 又∵
 面
面 ,∴
,∴ ,
,
由题设知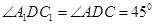 ,∴
,∴ =
= ,即
,即 ,
,
又∵ , ∴
, ∴ ⊥面
⊥面 , ∵
, ∵
 面
面 ,
,
∴面 ⊥面
⊥面 ;
;
(Ⅱ)设棱锥 的体积为
的体积为 ,
, =1,由题意得,
=1,由题意得, =
= =
= ,
,
由三棱柱 的体积
的体积 =1,
=1,
∴ =1:1, ∴平面
=1:1, ∴平面 分此棱柱为两部分体积之比为1:1
分此棱柱为两部分体积之比为1:1
| f(x1)-f(x2) | 1+f(x1)f(x2) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com