
题目列表(包括答案和解析)
已知函数f(x)= 在x=0,x=
在x=0,x= 处存在极值。
处存在极值。
(Ⅰ)求实数a,b的值;
(Ⅱ)函数y=f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围;
(Ⅲ)当c=e时,讨论关于x的方程f(x)=kx(k∈R)的实根个数。
已知函数 的最小值为0,其中
的最小值为0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的 有
有 ≤
≤ 成立,求实数
成立,求实数 的最小值;
的最小值;
(Ⅲ)证明 (
( ).
).
【解析】(1)解:
 的定义域为
的定义域为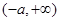

由 ,得
,得
当x变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
因此, 在
在 处取得最小值,故由题意
处取得最小值,故由题意 ,所以
,所以
(2)解:当 时,取
时,取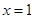 ,有
,有 ,故
,故 时不合题意.当
时不合题意.当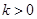 时,令
时,令 ,即
,即

令 ,得
,得
①当 时,
时, ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上单调递减.从而对于任意的
上单调递减.从而对于任意的 ,总有
,总有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合题意.
符合题意.
②当 时,
时, ,对于
,对于 ,
, ,故
,故 在
在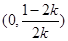 上单调递增.因此当取
上单调递增.因此当取 时,
时, ,即
,即 不成立.
不成立.
故 不合题意.
不合题意.
综上,k的最小值为 .
.
(3)证明:当n=1时,不等式左边= =右边,所以不等式成立.
=右边,所以不等式成立.
当 时,
时,


在(2)中取 ,得
,得
 ,
,
从而

所以有





综上,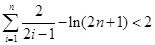 ,
,
(12分)已知函数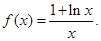
(1)设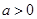 ,若函数在区间
,若函数在区间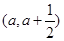 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(2)如果当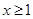 时,不等式
时,不等式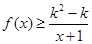 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
已知函数f(x)= 在x=0,x=
在x=0,x= 处存在极值。
处存在极值。
(Ⅰ)求实数a,b的值;
(Ⅱ)函数y=f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围;
(Ⅲ)当c=e时,讨论关于x的方程f(x)=kx(k∈R)的实根个数。
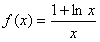 ,
,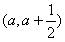 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;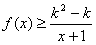 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
一、选择题
1―5 CADBA 6―10 CBABD 11―12 CC
二、填空题
13.(理) (文)(―1,1) 14.
(文)(―1,1) 14. 15.(理)18(文)(1,0)
15.(理)18(文)(1,0)
16.①③
三、解答题
17.解:(1)由题意得 ………………2分
………………2分

(2)由 可知A、B都是锐角, …………7分
可知A、B都是锐角, …………7分

这时三角形为有一顶角为120°的等腰三角形 …………12分
18.(理)解:(1)ξ的所有可能的取值为0,1,2,3。 ………………2分

(2) ………………12分
………………12分
(文)解:(1) ; ………………6分
; ………………6分
(2)因为
 …………10分
…………10分
所以 …………12分
…………12分
19.解:(1) , ………………1分
, ………………1分
依题意知, ………………3分
………………3分
(2)令 …………4分
…………4分
 …………5分
…………5分
所以, …………7分
…………7分
(3)由上可知
①当 恒成立,
恒成立,
必须且只须 , …………8分
, …………8分
 ,
,
则 ………………9分
………………9分
②当 ……10分
……10分
要使当
综上所述,t的取值范围是 ………………12分
………………12分
20.解法一:(1)取BB1的中点D,连CD、AD,则∠ACD为所求。…………1分

(2)方法一 作CE⊥AB于E,C1E1⊥A1B1于E1,连EE1,
则AB⊥面CC1E1E,因此平面PAB⊥面CC1E1E。
因为A1B1//AB,所以A1B1//平面PAB。则只需求点E1到平面PAB的距离。
作E1H⊥EP于H,则E1H⊥平面PAB,则E1H即为所求距离。 …………6分
求得 …………8分
…………8分
方法二:设B1到平面PAB的距离为h,则由
得 ………………8分
………………8分
(3)设平面PAB与平面PA1B1的交线为l,由(2)知,A1B1//平面PAB,
则A1B1//l,因为AB⊥面CC1E1E,则l⊥面CC1E1E,
所以∠EPE1就是二面有AB―P―A1B的平面角。 ………………9分
要使平面PAB⊥平面PA1B1,只需∠EPE1=90°。 ………………10分
在矩形CEE1C1中,
解得
|