题目列表(包括答案和解析)
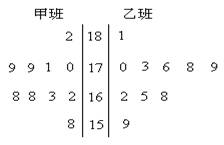
（本小题满分12分）某市教育局责成基础教育处调查本市学生的身高情况，基础教育处随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示：
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差；
(3)现从各班身高最高的5名同学中各取一人，求甲班同学身高不低于乙班同学的概率.
（本小题满分12分）某大学高等数学老师这学期分别用
两种不同的教学方式试验甲、乙两个大一新班（人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）.现随机抽取甲、乙两班各20名的高等数学期末考试成绩，得到茎叶图：（Ⅰ）依茎叶图判断哪个班的平均分高？
（Ⅱ）现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学，求成绩为86分的同学至少有一个被抽中的概率；
（Ⅲ）学校规定：成绩不低于85分的为优秀，请填写下面的
列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
下面临界值表仅供参考：
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：
其中
）
（本小题满分12分）
某科考试中，从甲、乙两个班级各抽取10名同学的成绩进行统计分析，两班成绩的茎叶图如图5所示，成绩不小于90分为及格．
| 甲 | 乙 | |
| 257 368 58 68 | 7 8 9 10 | 89 678 1235 1 |
（Ⅰ）甲班10名同学成绩的标准差 乙班10名同学成绩的标准差（填“>”，“<”）；
（Ⅱ）从两班10名同学中各抽取一人，已知有人及格，求乙班同学不及格的概率；
（Ⅲ）从甲班10人中取一人，乙班10人中取两人，三人中及格人数记为X，
|
（本小题满分12分）
某科考试中，从甲、乙两个班级各抽取10名同学的成绩进行统计分析，两班成绩的茎叶图如图3所示，成绩不小于90分为及格．
（Ⅰ）甲班10名同学成绩标准差 乙班10名同学成绩标准差（填“>”，“<”）；
（Ⅱ）从甲班4名及格同学中抽取两人，从乙班2名80分以下的同学中取一人，求三人平均分不及格的概率.
| 甲 | 乙 | |
| 257 368 24 68 | 7 8 9 10 | 89 678 1235 1 |
（本小题满分12分）某大学高等数学老师这学期分别用
两种不同的教学方式试验甲、乙两个大一新班（人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）.现随机抽取甲、乙两班各20名的高等数学期末考试成绩，得到茎叶图：（Ⅰ）依茎叶图判断哪个班的平均分高？
（Ⅱ）现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学，求成绩为86分的同学至少有一个被抽中的概率；
（Ⅲ）学校规定：成绩不低于85分的为优秀，请填写下面的
列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
下面临界值表仅供参考：
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：
其中
）
一．选择题
1.B 2.B 3. A 4.A 5.C 6. D 7.B 8.D 9.B 10.A 11.C 12.C
二．填空题
13.(1, 
)∪( ,2)
14.
15.
16. ②③④
三.解答题
17.解：（1）两学生成绩绩的茎叶图如图所示……………4分
(2)将甲、乙两学生的成绩从小到大排列为：
甲: 512 522 528 534 536 538 541 549 554 556
乙:515 521 527 531 532 536 543 548 558 559
从以上排列可知甲学生成绩的中位数为
……6分
乙学生成绩的中位数为
…………8分
甲学生成绩的平均数为:
……………10分
乙学生成绩的平均数为:
……………12分
18.解:（1）∵
∴
，
∴
，∴
∵ 
∈(0,π)
∴
……4分
（2）∵
∴
，即
① …………6分
又
∴
，即
② …………8分
由①②可得
，∴
………………………………………10分
又
∴
， ……………………………………12分
高三数学试题答案（文科）（共4页）第1页
19.（I）设
是
的中点，连结
，则四边形
为正方形，……………2分
．故
，
，
，
，即
．
………………………4分
又
，
平面
，…………………………6分
（II）证明：DC的中点即为E点， ………………………………………………8分
连D1E,BE
∴四边形ABED是平行四边形，
∴AD
BE,又ADA1D1 
A1D1 ∴四边形A1D1EB是平行四边形 
D1E//A1B ,
∵D1E
平面A1BD ∴D1E//平面A1BD。……………………………………………12分
20.解：（1）设这二次函数f(x)＝ax2+bx (a≠0) ,则
得a=3 , b=－2, 所以 f(x)＝3x2－2x. ……………………………………3分
又因为点
均在函数
的图像上，所以
＝3n2－2n.
当n≥2时，an＝Sn－Sn－1＝（3n2－2n）－
＝6n－5.
当n＝1时，a1＝S1＝3×12－2＝6×1－5，所以，an＝6n－5 （
）………6分
（2）由（1）得知
＝
＝
，……8分
故Tn＝
＝
＝（1－
）………10分
因此，要使（1－
）<
（）成立的m,必须且仅须满足
≤，即m≥10，所以满足要求的最小正整数m为10. ………………………12分
|
由-1≤a≤1的一切a的值，都有g(x)＜0
＜x＜1 …………6分
时,
， 函数y=f(x)的图像与直线y=3只有一个公共点，
的图像与x轴只有一个公共点。………8分
知,
点取得极大值,在x=
<m<0或0<m<
,则
.
……………………4分
，联立方程有
， ∵直线l与椭圆交于A．B两个不同点，
…………8分
，
由
