
题目列表(包括答案和解析)
(文)已知t>0,则关于x的方程![]() 有相异实根的个数是 ( )
有相异实根的个数是 ( )
A.0或2个 B.0或2或4个 C.0或2或3或4个 D.0或1或2或3或4个
(文)某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
|
|
A |
B |
C |
D |
E |
|
第一次通话时间 |
3分 |
3分45秒 |
3分55秒 |
3分20秒 |
6分 |
|
第二次通话时间 |
0分 |
4分 |
3分40秒 |
4分50秒 |
0分 |
|
第三次通话时间 |
0分 |
0分 |
5分 |
2分 |
0分 |
|
应缴话费(元) |
|
|
|
|
|
(1)在上表中填写出各人应缴的话费;
(2)设通话时间为t分钟,试根据上表完成下表的填写(即这五人在这一天内的通话情况统计表):
|
时间段 |
频数累计 |
频数 |
频率 |
累计频率 |
|
0<t≤3 |
┯ |
2 |
0.2 |
0.2 |
|
3<t≤4 |
|
|
|
|
|
4<t≤5 |
|
|
|
|
|
5<t≤6 |
|
|
|
|
|
合计 |
正 正 |
|
|
|
(3)若该本地网营业区原来执行的电话收费标准是:每3分钟为0.20元(不足3分钟按3分钟计算)。问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比,是增多了还是减少了?增或减了多少?
(文)某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
| | A | B | C | D | E |
| 第一次通话时间 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通话时间 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通话时间 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 应缴话费(元) | | | | | |
| 时间段 | 频数累计 | 频数 | 频率 | 累计频率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | | | | |
| 4<t≤5 | | | | |
| 5<t≤6 | | | | |
| 合计 | 正 正 | | | |
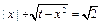 有相异实根的个数是( )
有相异实根的个数是( )| A.0或2个 | B.0或2或4个 | C.0或2或3或4个 | D.0或1或2或3或4个 |
| | A | B | C | D | E |
| 第一次通话时间 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通话时间 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通话时间 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 应缴话费(元) | | | | | |
| 时间段 | 频数累计 | 频数 | 频率 | 累计频率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | | | | |
| 4<t≤5 | | | | |
| 5<t≤6 | | | | |
| 合计 | 正 正 | | | |
一、选择题:本大题12个小题,每小题5分,共60分.
BBDDC DA CDA CA
二、填空题:本大题共4个小题,每小题4分,共16分.
13、i≥11,或i>10; 14、2 ; 15、2 ;16.①②试题.files/image168.gif) ③④ ①③
③④ ①③试题.files/image168.gif) ②④
②④
三、解答题:本大题共6个小题,满分74分.
17.解∵试题.files/image129.gif) =
=试题.files/image172.gif)
试题.files/image133.gif) =
=试题.files/image135.gif) ∴
∴试题.files/image129.gif) +
+试题.files/image133.gif) =
=试题.files/image177.gif)
故f(x)=(试题.files/image129.gif) +
+试题.files/image133.gif) )?
)?试题.files/image133.gif) +k=
+k=试题.files/image179.gif)
=试题.files/image181.gif)
=试题.files/image183.gif) …………………………4分
…………………………4分
(1)由题意可知试题.files/image185.gif) ,∴
,∴试题.files/image187.gif) 又
又试题.files/image137.gif) >1,∴0≤
>1,∴0≤试题.files/image137.gif) ≤1
……………………6分
≤1
……………………6分
(2)∵T=试题.files/image191.gif) ,∴
,∴试题.files/image137.gif) =1 ∴f (x)=sin(2x-
=1 ∴f (x)=sin(2x-试题.files/image193.gif) )+k+
)+k+试题.files/image146.gif)
∵x∈试题.files/image196.gif) ………………8分
………………8分
从而当2x-试题.files/image193.gif) =
=试题.files/image193.gif) 即x=
即x=试题.files/image193.gif) 时fmax(x)=f(
时fmax(x)=f(试题.files/image193.gif) )=sin
)=sin试题.files/image193.gif) +k+
+k+试题.files/image146.gif) =k+1=
=k+1=试题.files/image146.gif)
∴k=-试题.files/image146.gif) 故f (x)=sin(2x-
故f (x)=sin(2x-试题.files/image193.gif) )…………………12分
)…………………12分
18、(本小题满分12分)由a、b、c成等差数列
得a+c=2b 平方得a2+c2=4b2-
又S△ABC=试题.files/image150.gif) 且sin B=
且sin B=试题.files/image148.gif) , ∴S△ABC=
, ∴S△ABC=试题.files/image146.gif) ac? sin B=
ac? sin B=试题.files/image146.gif) ac×
ac×试题.files/image148.gif) =
=试题.files/image203.gif) ac=
ac=试题.files/image150.gif)
故ac=试题.files/image205.gif) ②………………………………………………………………………4分
②………………………………………………………………………4分
由①②可得a2+c2=4b2-试题.files/image207.gif) ③…………………………………………………5分
③…………………………………………………5分
又∵sin B=试题.files/image148.gif) ,且a、b、c成等差数列∴cos B=
,且a、b、c成等差数列∴cos B=试题.files/image209.gif) =
=试题.files/image211.gif) =
=试题.files/image213.gif) …………8分
…………8分
由余弦定理得: b2=a2+c2-试题.files/image205.gif) ×
×试题.files/image213.gif) =a2+c2-
=a2+c2-试题.files/image216.gif) ④………10分
④………10分
由③④可得 b2=4∴b=2………………….…12分
19、略解:(Ⅰ)∵数列{an}的前n项和为试题.files/image152.gif) ∴a1= S1=1…………(1分)
∴a1= S1=1…………(1分)
当n≥2时,an= Sn- Sn-1=n………………(3分) ∴an=n………………(4分)
(Ⅱ)由若b1=1,2bn-bn-1=0得试题.files/image218.gif) …………(5分)
…………(5分)
∴{bn}是以b1=1为首项,1/2为公比的等比数列. …………(6分)
试题.files/image220.gif) …………(8分) ∴
…………(8分) ∴试题.files/image222.gif) ………(9分)
………(9分)
试题.files/image224.gif) ………(10分)
………(10分)
两式相减得: 试题.files/image226.gif) ………(11分)
………(11分)
∴ Tn<4………(12分)
20、解:(I)将圆C配方得:(x+1)2+(y-2)2=2………………(1分)
试题.files/image228.gif)
试题.files/image230.gif)
试题.files/image232.gif) 21、解:(1)
21、解:(1)试题.files/image234.gif) Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN
试题.files/image168.gif) GQ为PN的中垂线
GQ为PN的中垂线试题.files/image168.gif) |PG|=|GN| …………2分
|PG|=|GN| …………2分
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长试题.files/image238.gif) ,半焦距
,半焦距试题.files/image240.gif) ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是试题.files/image242.gif) ……4分
……4分
(2)因为试题.files/image244.gif) ,所以四边形OASB为平行四边形
,所以四边形OASB为平行四边形
若存在l使得|试题.files/image246.gif) |=|
|=|试题.files/image248.gif) |,则四边形OASB为矩形
|,则四边形OASB为矩形试题.files/image250.gif)
若l的斜率不存在,直线l的方程为x=2,由试题.files/image252.gif)
试题.files/image254.gif) 矛盾,故l的斜率存在. …………6分
矛盾,故l的斜率存在. …………6分
设l的方程为试题.files/image256.gif)
试题.files/image258.gif)
试题.files/image260.gif) ①
①试题.files/image262.gif)
试题.files/image264.gif) ② …………10分
② …………10分
把①、②代入试题.files/image266.gif) ∴存在直线
∴存在直线试题.files/image268.gif) 使得四边形OASB的对角线相等. …12分
使得四边形OASB的对角线相等. …12分
22、解:(Ⅰ) 试题.files/image270.gif)
因为函数f(x)在区间[-1,1]上是增函数,所以f‘(x)≥0在区间x∈[-1,1]恒成立
即有x2-ax-2≤0在区间[-1,1]上恒成立。 构造函数g(x)=x2-ax-2
∴满足题意的充要条件是:试题.files/image272.gif)
所以所求的集合A[-1,1] ………(7分)
(Ⅱ)由题意得:试题.files/image274.gif) 得到:x2-ax-2=0………(8分)
得到:x2-ax-2=0………(8分)
因为△=a2+8>0 所以方程恒有两个不等的根为x1、x2由根与系数的关系有:试题.files/image276.gif) ……(9分)
……(9分)
因为a∈A即a∈[-1,1],所以试题.files/image278.gif) 要使不等式
要使不等式试题.files/image166.gif) 对任意a∈A及t∈[-1,1]恒成立,当且仅当
对任意a∈A及t∈[-1,1]恒成立,当且仅当试题.files/image280.gif) 对任意的t∈[-1,1]恒成立……(11分)
对任意的t∈[-1,1]恒成立……(11分)
构造函数φ(x)=m2+tm-2=mt+(m2-2) ≥0对任意的t∈[-1,1]恒成立的充要条件是
试题.files/image282.gif) m≥2或m≤-2.故存在实数m满足题意且为
m≥2或m≤-2.故存在实数m满足题意且为
{m| m≥2或m≤-2}为所求 (14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com